P12722 [KOI 2021 Round 2] 计算机器人

试题来源：。中文翻译做了少量本土化修改。 按照[署名—非商业性使用—相同方式共享 4.0 协议国际版](https://creativecommons.org/licenses/by-nc-sa/4.0/deed.zh-hans)进行授权。

在一个由 $M$ 行（横向）和 $N$ 列（纵向）组成的网格中，每一个格子里都有一个机器人。 每一行从上到下依次编号为 1 到 $M$，每一列从左到右依次编号为 1 到 $N$。通过这些编号，我们可以使用坐标 $(行\ 编号,\ 列\ 编号)$ 来表示网格中的格子位置。 每个机器人都有一个或多个输入值、一个存储值和一个输出值。 机器人的运作方式如下：从最左边一列的机器人开始，按列编号顺序依次运作。处于同一列中的机器人会同时运行。 机器人的行为如下（表达式 $|A|$ 表示整数 $A$ 的绝对值，即当 $A \geq 0$ 时 $|A| = A$，当 $A < 0$ 时 $|A| = -A$）： - 最左边一列的机器人，其输入值仅为一个 $0$。 - 坐标为 $(i, j)$ 的机器人的输入值，是所有满足 $|i - a| \leq j - b$ 且 $b < j$ 的坐标 $(a, b)$ 的机器人们的输出值。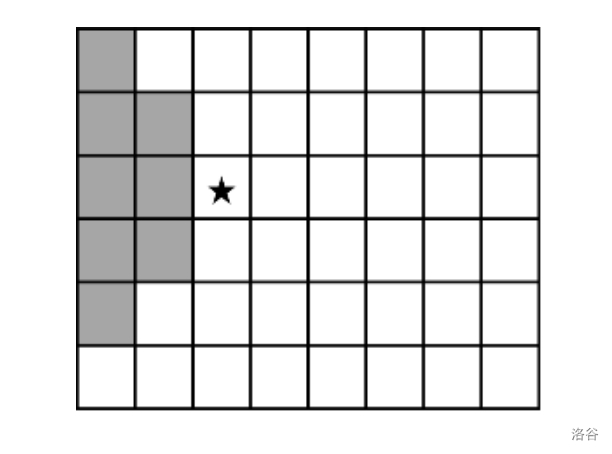  - 每个机器人将其所有输入值中的最大值，作为自己的存储值。 - 每个机器人将自己的存储值加上自己的权重 $D_{i,j}$，并将所得值作为其输出值。 请编写一个程序，读取机器人的权重信息，计算所有机器人的存储值中的最大值（即最大存储值）。

第一行包含两个整数 $M$ 和 $N$，中间用一个空格分隔。 接下来的 $M$ 行，每行包含一个长度为 $N$ 的字符串，表示对应行的每个机器人的权重。每个字符为一个数字，表示该格子中机器人的权重 $D_{i,j}$。

输出一行，即所有机器人存储值中的最大值。

**约束条件** - $1 \leq M \leq 2000$ - $1 \leq N \leq 2000$ - 对于所有满足 $1 \leq i \leq M$ 且 $1 \leq j \leq N$ 的 $(i,j)$，都有 $1 \leq D_{i,j} \leq 9$ **子任务** 1. （3 分）$N = 1$ 2. （8 分）$N = 2$ 3. （9 分）$M = 1$ 4. （21 分）$M \leq 100$ 且 $N \leq 100$ 5. （59 分）无额外约束条件