P12734 Understand

**We've provided some greater samples of this problem, you can download `samples.zip`. The files `sample2-4` satify the constraints of Subtasks 2-4.** > "Asamura-kun, you..."\ "**--You understand me too well.**"\ --Saki Ayase

Saki is practicing modern literature reading conprehension using the method recommended by Yuta. There are $n$ historical events, numbered from $1$ to $n$, where each event may have a prerequisite event with a smaller number, or it may have none. Formally, for event $i$, let $p_i$ denote the number of its prerequisite event, satisfying $p_i < i$. If $p_i = 0$, it means the event has no prerequisite. Saki has two ways to recall a historical event: recollection and association. If she recollects, she can spend $r_u$ time to recall event $u$. If she associates, she can choose any event $u$ that she has already recalled and spend $t_v$ time to recall an event $v$ where $p_v = u$. However, her brain capacity is limited, so she can only recall up to $k$ events simultaneously. She can choose to forget any event she has already recalled at any moment, and forgetting an event does not take any time. To prevent memory confusion, she will not recall any events she has previously forgotten. Now, she has $m$ reading questions, and the $i$-th question requires her to recall event $x_i$. She can solve the $i$-th problem immediately upon recalling event $x_i$, and the time taken is negligible. She wants to know the minimum amount of time she needs to spend to solve all the questions.

The first line contains an integer $T$, denoting the number of test cases. For each test case, the first line contains three integers, $n,m$ and $k$, representing the number of historical events, the number of reading questions, respectively and the number of events that she can recall at the same time. The second line is consisted of $n$ integers representing $p_1,\dots,p_n$. The third line is consisted of $n$ integers representing $r_1,\dots,r_n$. The fourth line is consisted of $n$ integers representing $t_1,\dots,t_n$. It is guaranteed that when $p_i=0$, $t_i=0$. The fifth line is consisted of $m$ integers representing $x_1,\dots,x_m$.

For each test case, output a single integer on a line indicating the minimum amount of time she needs to spend to solve all the questions.

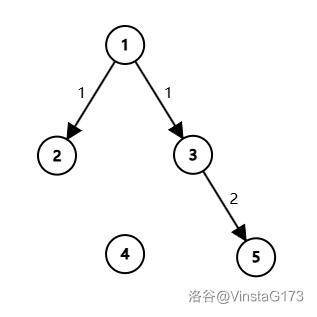
#### Sample Explanation For the first test case, the relationships between historical events form the graph as below:  She can perform the following recollection process: | Step | Process | Time Taken | Set of Recalled Events | Question Solved | | :-: | :-: | :-: | :-: | :-: | | $1$ | Recollects Event $1$ | $1$ | $\{1\}$ | | | $2$ | Associates Event $3$ | $1$ | $\{1,3\}$ | | | $3$ | Associates Event $5$ | $2$ | $\{1,3,5\}$ | $3$ | | $4$ | Forgets Event $3$ | $0$ | $\{1,5\}$ | | | $5$ | Associates Event $2$ | $1$ | $\{1,2,5\}$ | $1$ | | $6$ | Forgets Event $2$ | $0$ | $\{1,5\}$ | | | $7$ | Recollects Event $4$ | $4$ | $\{1,4,5\}$ | $2$ | Total time taken: $1+1+2+1+4=9$. #### Constraints **This problem enables subtask scoring, with the constraints and scores for each subtask as follows.** | Subtask No. | $n,m\le$ | Special Constraint | Score | Depends on Subtask | | :-: | :-: | :-: | :-: | :-: | | $1$ | $10$ | | $18$ | | | $2$ | $10^5$ | A | $18$ | | | $3$ | $10^5$ | B | $18$ | | | $4$ | $10^5$ | C | $18$ | | | $5$ | $10^5$ | | $28$ | $1,2,3,4$ | Special constraint A: $p_i=0$ or $p_i=i-1$; Special constraint B: $p_i=\lfloor\frac i2\rfloor$; Special constraint C: $p_i\le1$. For all of the testdata, $1\le T\le5$, $1\le n,m\le10^5$, $1\le k\le10$, $0\le p_i