P12739 [POI 2016 R2] 快打砖块 Arkanoid

翻译来自于 [LibreOJ](https://loj.ac/p/5035)。

**题目译自 [XXIII Olimpiada Informatyczna — II etap](https://sio2.mimuw.edu.pl/c/oi23-2/dashboard/) [Arkanoid](https://szkopul.edu.pl/problemset/problem/O730xgZEVynTWBmscBinhMbD/statement/)** Arkanoid 是一款经典的电脑游戏，玩家通过移动一块挡板，反弹在游戏区域内移动的小球，用以击碎区域中的砖块。目标是击碎所有砖块。熟悉这款游戏的玩家都知道，击碎最后几块砖块往往既耗时又令人抓狂。因此，编写一个程序，根据初始游戏区域布局，计算赢得游戏所需的时间，将大有裨益。为简化问题，我们假设玩家操作完美无瑕，总能用挡板中心精准反弹小球。 游戏区域为长 $m$、高 $n$ 的矩形，其中 $m$ 为奇数，且 $m$ 与 $n$ 互质。区域上定义了一个直角坐标系：左下角为 $(0, 0)$，右上角为 $(m, n)$。为简化模型，假设小球尺寸可忽略，挡板厚度也可忽略。挡板沿直线 $y=0$ 水平移动，小球初始位于点 $\left(\frac{m}{2}, 0\right)$，初始速度向量为 $\left(-\frac{1}{2}, \frac{1}{2}\right)$。 当小球触碰到挡板、区域边界或任意砖块时，会发生完全弹性碰撞。此外，被触碰的砖块将被击碎并从区域中消失。请计算经过多少时间单位，所有砖块被击碎。

第一行包含三个整数 $m, n, k$ $(m, n, k \geq 1, k \leq n m - 1)$，分别表示游戏区域的宽度、高度和初始砖块数量。 接下来的 $k$ 行描述砖块位置，第 $i$ 行包含两个整数 $x_i, y_i$ $(1 \leq x_i \leq m, 1 \leq y_i \leq n)$，表示存在一块砖块，其为对角顶点为 $(x_i - 1, y_i - 1)$ 和 $(x_i, y_i)$ 的矩形。保证位置 $(x_i = \frac{m+1}{2}, y_i = 1)$ 处无砖块。

输出一行，包含一个整数，表示所有砖块被击碎所需的时间单位数。

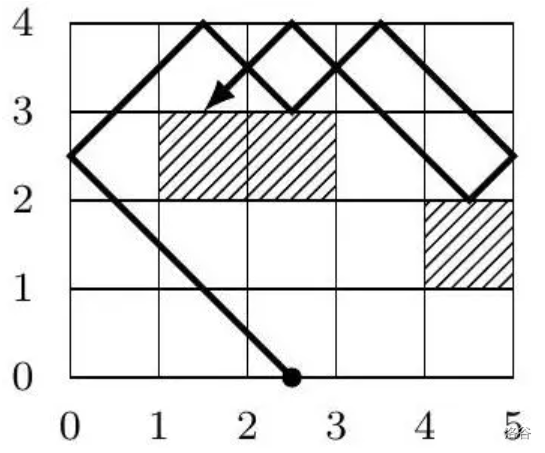
**样例 1 解释**  **附加样例** 1. $m=5, n=4, k=2$，答案较大。 2. $m=11, n=10$，砖块构成不触碰区域边界的棋盘格布局。 3. $m=99999, n=100000$，砖块位于 $\left(\frac{m-1}{2}, 2\right), \left(\frac{m-5}{2}, 2\right), \left(\frac{m-9}{2}, 2\right), \ldots$。 4. $m=99999, n=100000$，仅一块砖块位于 $(1, 1)$，答案较大。 详细子任务附加限制及分值如下表所示。 | 子任务 | 附加限制 | 分值 | | :---: | :--: | :---: | | $1$ | $m, n \leq 100, k \leq 1000$ | $25$ | | $2$ | $n, m \leq 100000, k \leq 50$ | $25$ | | $3$ | $m, n, k \leq 100000$，砖块互不直接接触且不触碰区域边界 | $25$ | | $4$ | $m, n, k \leq 100000$ | $25$ |