P1273 Cable Television Network

A pay cable television network plans to rebroadcast an important football match. Their rebroadcast network and user terminals form a tree structure. The root of the tree is located at the match venue, the leaves are user terminals, and the other relay stations are internal nodes of the tree. The signal transmission costs from relay station to relay station and from relay station to user terminals are known. The total cost of one broadcast equals the sum of all transmission costs used. Each user has prepared a certain amount of money to watch the match. The cable network has the right to decide which users receive the signal and which do not. Write a program to find a plan that allows the cable network to serve as many users as possible without incurring a loss.

The first line contains two integers $N$ and $M$ separated by a space, where $2 \le N \le 3000$, $1 \le M \le N - 1$. Here $N$ is the total number of nodes in the entire cable network, and $M$ is the number of user terminals. The first relay station (the root of the tree) is numbered $1$. The other relay stations are numbered from $2$ to $N - M$. The user terminals are numbered from $N - M + 1$ to $N$. The next $N - M$ lines each describe one relay station. The $(i + 1)$-th line describes relay station $i$ in the following format: $K \ \ A_1 \ \ C_1 \ \ A_2 \ \ C_2 \ \ \ldots \ \ A_k \ \ C_k$ $K$ indicates that this relay station has $K$ direct children (relay stations or users). Each child is given by a pair of integers $A$ and $C$, where $A$ is the child node number, and $C$ is the transmission cost from the current relay station to node $A$. The last line contains, in order, the amounts of money each user is willing to pay to watch the match. Each single transmission cost and each user's payment do not exceed $10$.

Output a single integer on one line: the maximum number of users that can be served without the network incurring a loss.

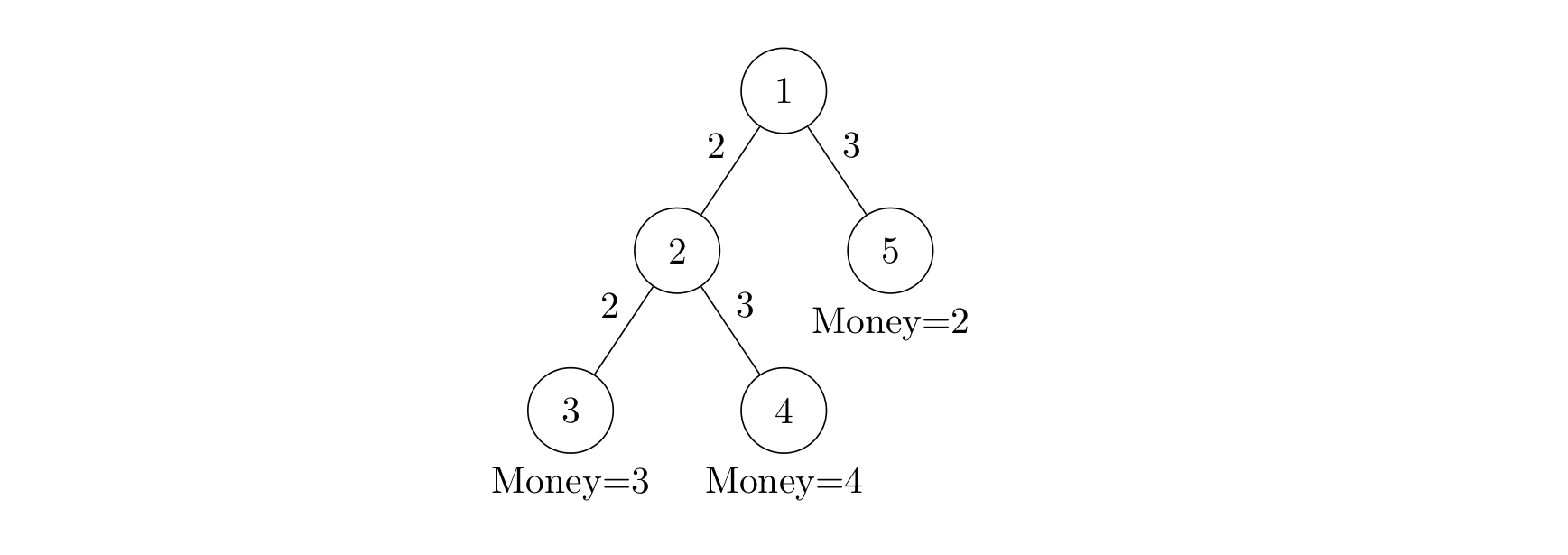
Sample explanation:  As shown in the figure, there are five nodes in total. Node 1 is the root node, i.e., the live broadcast station. Node 2 is a relay station. Nodes 3, 4, 5 are user terminals, $M$ in total, numbered from $N - M + 1$ to $N$. They are willing to pay $3$, $4$, and $2$, respectively. From node 1, the signal can be sent to node 2 at a cost of $2$; it can also be sent to node 5 at a cost of $3$ (as shown by the second line of data). From node 2, the signal can be sent to node 3 at a cost of $2$; it can also be sent to node 4 at a cost of $3$ (as shown by the third line of data). If all users (3, 4, 5) are to watch the match, the total transmission cost is $2 + 3 + 2 + 3 = 10$, which is greater than the total amount users are willing to pay $3 + 4 + 2 = 9$, so the cable network would incur a loss. If only users 3 and 4 watch the match, then there is no loss. Translated by ChatGPT 5