P12754 [POI 2017 R3] 米达斯 Midas

翻译来自于 [LibreOJ](https://loj.ac/p/5062)。

**题目译自 [XXIV Olimpiada Informatyczna — III etap](https://sio2.mimuw.edu.pl/c/oi24-3/dashboard/) [Midas](https://szkopul.edu.pl/problemset/problem/wrTmzO9-dzEbLtsRUCdMV2_W/statement/)** Bajtazar，米达斯国王的御用工程师，奉命建造了一座迷宫。原计划迷宫的房间用于展示珍奇展品，但实际上，它成了为国王金库增收巨额金币的工具。 迷宫由多个房间和连接它们的通道组成，入口位于房间 $1$。每间房间的通道分叉，可选择左或右通道离开（部分通道可能被封锁，无法通行）。通道只分叉，不汇合。游客携带收费装置，每次通过通道需支付金币，费用取决于已付金币总数及所选通道：左通道费用等于此前总费用，右通道费用比此前总费用多 $1$ 金币。 这种复杂的收费机制旨在掩盖实际游览成本，但给游客带来不便。Bajtazar 决定协助游客，聘请你编写程序回答以下查询：若游客持有恰好从入口到房间 $x$ 所需的金币，能否用同样金币从入口到达房间 $y$？

第一行包含一个正整数 $n$，表示迷宫房间数量，房间编号为 $1$ 至 $n$，入口位于房间 $1$。 接下来的 $n$ 行描述迷宫，第 $i$ 行包含两个整数 $l_i, r_i$ $(0 \leq l_i, r_i \leq n)$。若 $l_i > 0$，表示从房间 $i$ 的左通道可达房间 $l_i$；若 $l_i = 0$，左通道被封锁。$r_i$ 类似描述右通道。从房间 $1$ 出发，可达所有其他房间。 下一行包含一个正整数 $z$，表示查询数量。 接下来的 $z$ 行描述查询，第 $i$ 行包含两个整数 $x_i, y_i$ $(1 \leq x_i, y_i \leq n)$，表示查询：从入口到房间 $x_i$ 所需金币是否足够到达房间 $y_i$。

输出 $z$ 行，若第 $i$ 个查询的答案为是，在第 $i$ 行输出 `TAK`，否则输出 `NIE`。

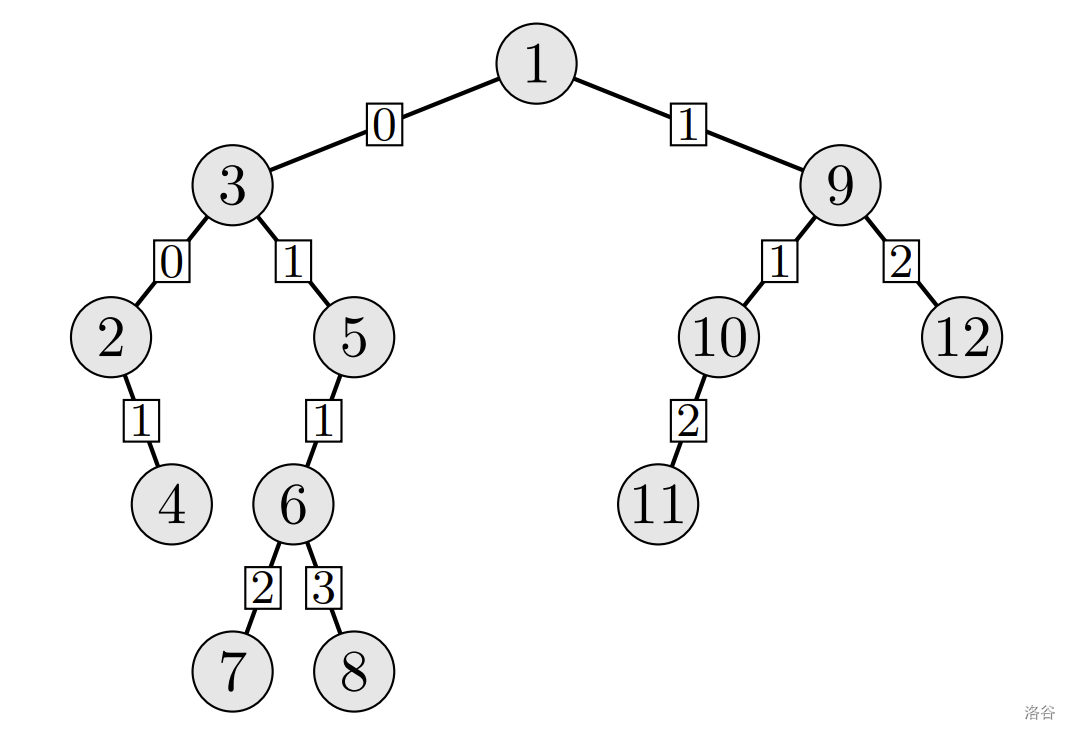
**样例 1 解释**  图示描绘了示例中的迷宫：房间用圆圈表示，通道费用标注于方框内。从上至下、选择左或右分支对应迷宫中的左或右路。例如，访问房间 $3$ 需支付 $3+1+1+1=3+3$ 金币；访问房间 $11$ 需支付 $1+1+3+1=4$ 金币，不足以到达房间 $8$（需 $0+1+1+2=5$ 金币），对应第一个查询的 `NIE`。 **附加样例** 1. $n=7$，房间形成完全二叉树，$z=49$，查询所有房间对。 2. $n=2^{15}-1$，房间形成完全二叉树，$z=n+1$，查询相邻叶子对，每对有两次查询（一次 `TAK`，一次 `NIE`）。 3. $n=1000000$，左路形成长度 $n/2$ 的路径，每房间有右通道分支，$z=10$，随机查询。 详细子任务附加限制及分值如下表所示。 | 子任务 | 附加限制 | 分值 | | :---: | :--: | :---: | | $1$ | $n \leq 20, z \leq 50$ | $15$ | | $2$ | $n \leq 1000, z \leq 1000$ | $9$ | | $3$ | $n \leq 1000, z \leq 1000000$ | $14$ | | $4$ | $n \leq 1000000, z \leq 1000$ | $11$ | | $5$ | $n \leq 1000000, z \leq 1000000$ | $51$ |