P12761 [POI 2018 R2] 列车员 Conductor

翻译来自于 [LibreOJ](https://loj.ac/p/5069)。

**题目译自 [XXV Olimpiada Informatyczna — II etap](https://sio2.mimuw.edu.pl/c/oi25-2/dashboard/) [Konduktor](https://szkopul.edu.pl/problemset/problem/lbADmW7d353d0F0iw4kXTjsl/statement/)** Bajtazar 是拜托尼亚最热门铁路线的列车员。这条线路途经 $m$ 个车站，编号从 $1$ 至 $m$。乘客可在任意车站上下车，为确保所有人持有效票，Bajtazar 需在每对连续车站间查票，但这显然效率低下。 为此，他决定更系统地解决问题。他选出 $n$ 条最热门的乘客路线，每条路线以一对 $a_i, b_i$ 表示，意为乘客在车站 $a_i$ 上车，$b_i$ 下车。Bajtazar 希望以最少的查票次数，确保每条路线上的乘客至少被查一次，即每条路线 $a_i$ 至 $b_i$ 间至少有一次查票。查票不得在车站停靠时进行。 此外，固定查票时机不明智。常客若摸清规律，可能调整路线避开查票。因此，Bajtazar 还想知道所有可能的查票方案。两方案不同，若存在一对连续车站，在一方案中查票而在另一方案中不查。为初步了解，他需计算方案数对 $1000000007$ 取模的结果。

第一行包含一个整数 $z$ $(z \geq 1)$，表示测试数据组数。随后为各组描述。 每组第一行包含两个整数 $m, n$ $(1 \leq m \leq 10^9, 1 \leq n)$，分别表示车站数和路线数。 接下来的 $n$ 行描述路线，第 $i$ 行包含两个整数 $a_i, b_i$ $(1 \leq a_i < b_i \leq m)$，表示第 $i$ 条路线从车站 $a_i$ 上车，$b_i$ 下车。每对有序对 $(a_i, b_i)$ 至多出现一次。

输出 $z$ 行，每行对应一组测试数据，包含两个整数，分别表示满足 Bajtazar 要求的最少查票次数及查票方案数对 $1000000007$ 取模。

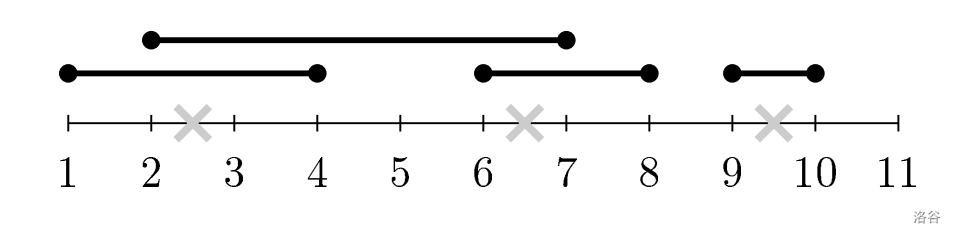
**样例 1 解释**  第一组测试需覆盖四条路线，至少查票三次。一种方案在车站 $2,6,9$ 离站后查票，其余方案为 $\{2,7,9\}, \{3,6,9\}, \{3,7,9\}, \{1,6,9\}$，共五种。第二组测试需覆盖两条路线，至少查票两次，仅一种方案。 **附加样例** 1. $n=4, m=10$。 2. $n=3000$，路线 $i$ 与 $i+1$ 相交，$i=1,\ldots,n-1$。 3. $n=100000$，所有路线区间互不包含。 4. $n=100000$，一次查票可覆盖所有乘客。 所有附加样例中 $z=1$。 $N$ 为所有 $z$ 组测试数据的 $n$ 之和。若程序仅正确输出最少查票次数（每行仍需输出两个整数，第二个整数为 $32$ 位有符号整数），可获 $20\%$ 分数。 详细子任务附加限制及分值如下表所示。 | 子任务 | 附加限制 | 分值 | | :---: | :--: | :---: | | $1$ | $z \leq 10, n \leq 15$ | $10$ | | $2$ | $z \leq 100, N \leq 5000$ | $10$ | | $3$ | $z \leq 100, N \leq 500000$，至多三次查票可覆盖所有乘客 | $15$ | | $4$ | $z \leq 100, N \leq 500000$，任意三路线区间交集为空 | $15$ | | $5$ | $z \leq 100, N \leq 500000$ | $50$ |