P12776 [POI 2018/2019 R1] 小机器人 Robby the little robot

翻译来自于 [LibreOJ](https://loj.ac/p/4922)。

**题目译自 [XXVI Olimpiada Informatyczna – I etap](https://sio2.mimuw.edu.pl/c/oi26-1/dashboard/) [Robocik](https://sio2.mimuw.edu.pl/c/oi26-1/p/rob/)** 想象一个带有直角坐标系的平面。在坐标 $(0,0)$ 处，有一个朝北（即 $y$ 坐标增大的方向）的小机器人等着你的指令。你可以通过一个命令序列 $d_{1}, d_{2}, \ldots, d_{n}$ 来编程控制它。启动后，机器人会按顺序执行动作：第 $i$ $(i \geq 1)$ 次移动时，它会向前走 $d_{((i-1) \bmod n)+1}$ 个单位，然后向右转 $90^\circ$。 机器人有块电池，能支持它运行 $t$ 秒。无论是移动一个单位还是转 $90^\circ$，都耗时 $1$ 秒。 请你写一个程序，算出在电池耗尽前，机器人会在指定点 $(x, y)$ 上出现多少次。

输入的第一行包含两个整数 $n$ 和 $t$ $(1 \leq n \leq 100000, t \geq 1)$，分别表示命令序列的长度和电池运行时间。 第二行包含 $n$ 个整数 $d_{1}, \ldots, d_{n}$ $(1 \leq d_{i} \leq 10^{9})$，表示命令序列中的移动距离。 第三行包含两个整数 $x$ 和 $y$ $(-10^{9} \leq x, y \leq 10^{9})$，表示我们要查询的点的坐标。

输出一个整数，表示机器人到达点 $(x, y)$ 的次数。如果它在时间 $0$ 或 $t$ 时位于该点，也要计入。

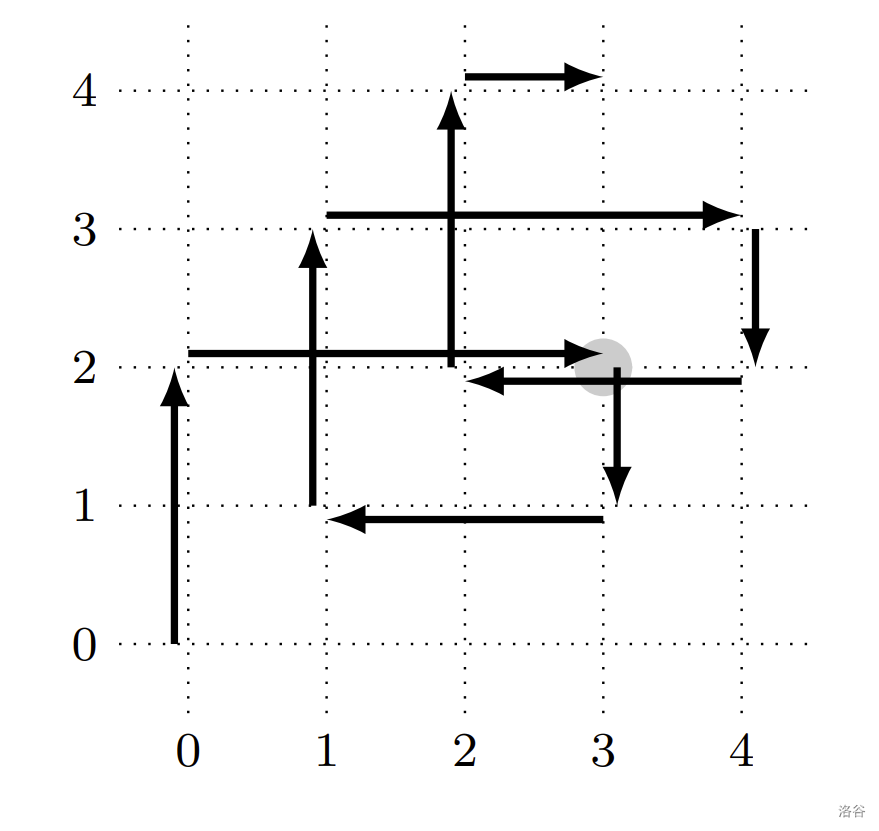
**样例 1 解释** 机器人会在启动后的第 $6$ 秒和第 $22$ 秒到达点 $(3,2)$。其路径如下图所示。  **附加样例** 1. 跟样例相同，但 $t=21$； 2. $n=1$ 的样例； 3. 大型螺旋样例，$d_{i}=i, n=31, t=\frac{10^{18}-1}{3}$。 详细子任务附加限制及分值如下表所示。 | 子任务 | 附加限制 | 分值 | | :---: | :--: | :---: | | $1$ | $t \leq 10^{6}$ | $10$ | | $2$ | $t \leq 10^{12}, 10^{6} \leq d_{i}$ | $30$ | | $3$ | $t \leq 10^{18}$ | $60$ |