P12783 [ICPC 2024 Yokohama R] The Farthest Point

译自 [ICPC 2024 Yokohama Regional Contest](https://icpc.jp/2024/)。

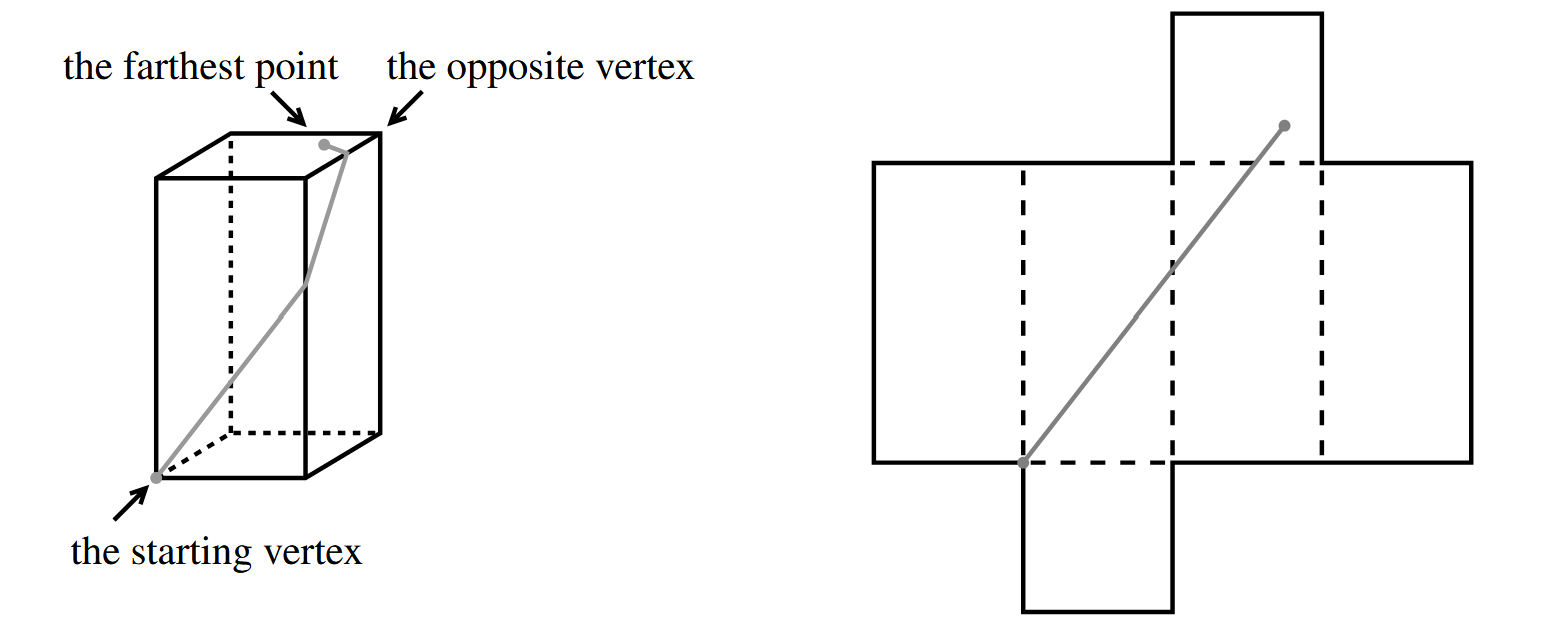
一只蚂蚁位于一个长方体的顶点之一，记作**起始顶点**。长方体（rectangular cuboid）是一个所有面均为矩形的六面体。对于这只蚂蚁而言，长方体的表面就构成了它的整个「世界」。 现在我们想知道：在长方体表面上，哪个点对于蚂蚁来说距离起始顶点最远。你可能会认为，**对角顶点**（即起始顶点的空间对角线的另一端顶点）就是最远的点。然而，对角顶点并不一定是最远的。 例如，对于一个尺寸为 $1 \times 1 \times 2$ 的长方体，其任一顶点到对角顶点的表面距离为 $\sqrt{8}$。而实际上，最远点到起始顶点的距离为 $\sqrt{\tfrac{65}{8}}$（见下图）。 >  > （$1\times 1\times 2$ 的长方体，和长方体的展开图） 现在给出长方体的边长尺寸。请编写一个程序，计算起始顶点到最远点的距离。

仅一组数据，格式如下所示： > $a$ $b$ $c$ 正整数 $a,b,c$ 表示长方体尺寸为 $a\times b\times c$。保证 $1\le a,b,c\le 100$。

输出一行一个实数，表示起始顶点到最远点的距离。相对误差不应大于 $10^{-9}$。