P12784 [ICPC 2024 Yokohama R] Beyond the Former Explorer

译自 [ICPC 2024 Yokohama Regional Contest](https://icpc.jp/2024/)。

**这是一道交互题。** 你正站在一片区域的正中心，该区域被划分为南北走向和东西走向的网格单元。一份巨大的宝藏隐藏在其中一个单元内。 John Belzoni——著名的宝藏猎人 Giovanni Battista Belzoni 的后裔——实际上已发现了这份宝藏。不幸的是，他在成功挖出宝藏前因中暑去世；他似乎花了过长的时间在这片区域徘徊。 John 的探索从你当前站立的区域中心单元出发。他通向宝藏的所有足迹都留在了这片区域，但只有抵达某个单元才能识别该单元上的足迹。某一单元上的足迹指示了他下一步前往四个相邻网格单元中的哪一个。 已知 John 不会重复访问同一网格单元。你在中心单元看到一个足迹，表明 **John 的第一步是向北**。 区域中存在恰好一个宝藏单元，只有站在该单元时你才能识别它。 下图展示了区域的一种可能情形。John 的足迹在单元中以箭头标识。宝藏单元标记为 $\texttt{G}$。阴影单元是你的初始位置。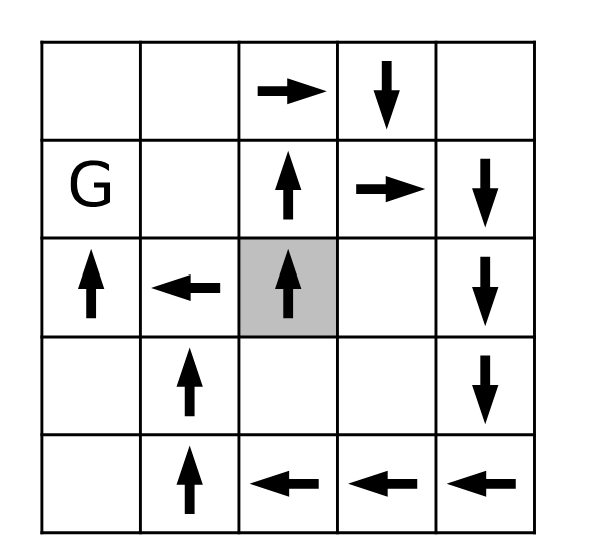  你的任务是在有限**步**内找到宝藏。每一步中，你需决定朝北、西、南、东四个方向之一移动，并进入该方向的相邻单元。当你移动到该单元时，可能发现宝藏、John 的足迹，或者空无一物。你无需追随 John 的足迹。与 John 的路线不同，你可以重复访问同一单元。无论你如何探索，John 的足迹始终保持不变。 ### 实现细节 交互开始时，你需从标准输入读取一个整数 $n$（$1 \leq n \leq 2000$），后接换行符。整数 $n$ 表示区域被划分为 $(2n + 1) \times (2n + 1)$ 的网格单元。你的初始位置从西向东第 $n+1$ 列、从北向南第 $n+1$ 行的单元。读入整数 $n$ 后，你即可开始探索。 每步，你向标准输出发送表示移动方向的单个字符： - `^`（插入符）表示向北； - ``（大于号）表示向东。 字符后需附加换行符。 作为回答，你将收到一个表示抵达单元内容的字符，后接换行符： - `G`：该单元有宝藏； - `^`, ``：John 的足迹分别指示北、西、南、东； - `.`（点号）：既无宝藏也无足迹。 当你发现宝藏（即收到 `G`）时，交互立即终止，你的程序必须退出。 **你需在 $\bf{30000}$ 步内抵达宝藏单元**。尽管追随 John 的足迹必能找到宝藏，但步数可能超过 $30000$。 以下情况将被判为 $\text{Wrong Answer}$： - 程序输出格式无效； - 指定了移出网格的方向； - 找到宝藏后仍有额外输出； - 未在 $30000$ 步内抵达宝藏单元。 区域的布局（宝藏位置与 John 的足迹）在交互前已固定，在交互过程中不会改变。 **在每次移动后，你都需要换行并刷新缓冲区**。例如： - $\texttt{C++}$ 中的 `cout.flush()`。

见「实现细节」。

见「实现细节」。

样例如「题目描述」中的图所示。