P12800 [NERC 2022] King' s Puzzle

King Kendrick is a sovereign ruler of Kotlin Kingdom. He is getting ready for the next session of the government. Kotlin Kingdom consists of $n$ cities. These cities need to be connected by several bidirectional roads. Since ministries are responsible for aspects of safety and comfort of the kingdom's residents, some of them have made the following requirements: - "All the cities should be connected by new roads, i.e. there should be a path from any city to any other city via the roads" --- Ministry of Transport and Digital Infrastructure. - "There may not be a loop road --- a road that connects a city with itself" --- Ministry of Environment. - "There should be at most one road between a pair of cities" --- Treasury Department. - "If $a_i$ is the number of roads connected to $i$-th city, then the set $\{a_1, \ldots, a_n\}$ should consist of exactly $k$ distinct numbers" --- Ministry of ICPC. King Kendrick has issues with the requirements from the Ministry of ICPC. He asks you to help him. Find any set of roads that suits all the requirements above or say that it is impossible.

The only line of the input consists of two integers $n$ and $k$ ($1 \le k \le n \le 500$).

If it is impossible to satisfy all the requirements, output $\texttt{NO}$ in the only line. Otherwise, output $\texttt{YES}$ in the first line. Output $m$ --- the number of roads ($0 \le m \le \frac{n \cdot (n - 1)}{2}$) in the second line. Next $m$ lines should contain pairs of integers $a$ and $b$ --- the cities to connect by a road ($1 \le a, b \le n$).

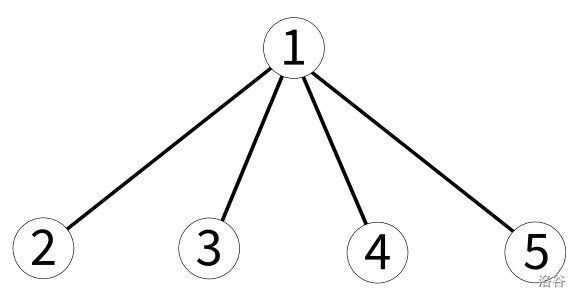
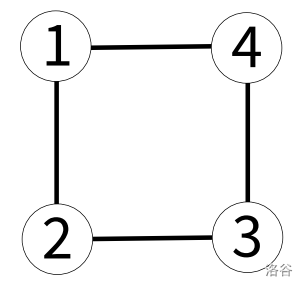
### Sample 1 Explanation  City 1 has four roads connected to it while other cities have exactly one. ### Sample 2 Explanation  Every city has exactly two roads connected to it.