P12800 [NERC 2022] King' s Puzzle

国王 Kendrick 是 Kotlin 王国的君主。他正在为下一次政$ $府会议做准备。Kotlin 王国由 $n$ 个城市组成。这些城市需要通过若干条双向道路连接起来。由于各个部门负责王国居民的安全和舒适等方面，其中一些部门提出了以下要求： - “所有城市都应通过新修的道路连接起来，即任意一个城市都应能通过道路到达其他任何城市”——交通与数字基础设施部。 - “不能有自环路——即连接一个城市到其自身的道路”——环境部。 - “任意一对城市之间最多只能有一条道路”——财政部。 - “如果 $a_i$ 是连接到第 $i$ 个城市的道路数量，那么集合 $\{a_1, \ldots, a_n\}$ 应恰好由 $k$ 个不同的数字组成”——ICPC 部。 国王 Kendrick 对 ICPC 部的要求感到头疼。他请求你帮助他。请找出一组满足上述所有要求的道路方案，或者说明这是不可能的。

输入的唯一一行包含两个整数 $n$ 和 $k$ ($1 \le k \le n \le 500$)。

如果无法满足所有要求，则在唯一一行输出 $\texttt{NO}$。 否则，在第一行输出 $\texttt{YES}$。 在第二行输出道路的数量 $m$ ($0 \le m \le \frac{n \cdot (n - 1)}{2}$)。 接下来的 $m$ 行应包含整数对 $a$ 和 $b$——表示要用道路连接的城市 ($1 \le a, b \le n$)。

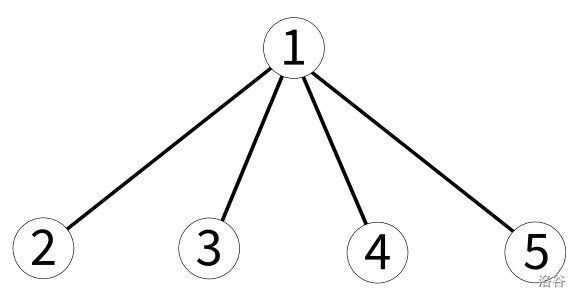
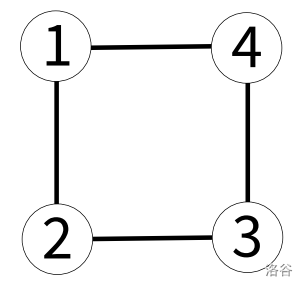
### 样例 1 解释  城市 1 有四条道路与之相连，而其他城市都只有一条。 ### 样例 2 解释  每个城市都恰好有两条道路与之相连。 翻译由 gemini2.5pro 完成