P12814 [NERC 2021] Admissible Map

A $\textit{map}$ is a matrix consisting of symbols from the set of $\texttt{U}$, $\texttt{L}$, $\texttt{D}$, and $\texttt{R}$. A $\textit{map graph}$ of a map matrix $a$ is a directed graph with $n \cdot m$ vertices numbered as $(i, j)$ ($1 \le i \le n; 1 \le j \le m$), where $n$ is the number of rows in the matrix, $m$ is the number of columns in the matrix. The graph has $n \cdot m$ directed edges $(i, j) \to (i + di_{a_{i, j}}, j + dj_{a_{i, j}})$, where $(di_U, dj_U) = (-1, 0)$; $(di_L, dj_L) = (0, -1)$; $(di_D, dj_D) = (1, 0)$; $(di_R, dj_R) = (0, 1)$. A map graph is $\textit{valid}$ when all edges point to valid vertices in the graph. An $\textit{admissible map}$ is a map such that its map graph is valid and consists of a set of cycles. A $\textit{description}$ of a map $a$ is a concatenation of all rows of the map --- a string $a_{1,1} a_{1,2} \ldots a_{1, m} a_{2, 1} \ldots a_{n, m}$. You are given a string $s$. Your task is to find how many substrings of this string can constitute a description of some admissible map. A $\textit{substring}$ of a string $s_1s_2 \ldots s_l$ of length $l$ is defined by a pair of indices $p$ and $q$ ($1 \le p \le q \le l$) and is equal to $s_ps_{p+1} \ldots s_q$. Two substrings of $s$ are considered different when the pair of their indices $(p, q)$ differs, even if they represent the same resulting string.

In the only input line, there is a string $s$, consisting of at least one and at most $20\,000$ symbols $\texttt{U}$, $\texttt{L}$, $\texttt{D}$, or $\texttt{R}$.

Output one integer --- the number of substrings of $s$ that constitute a description of some admissible map.

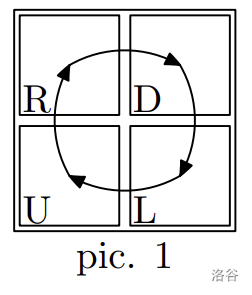
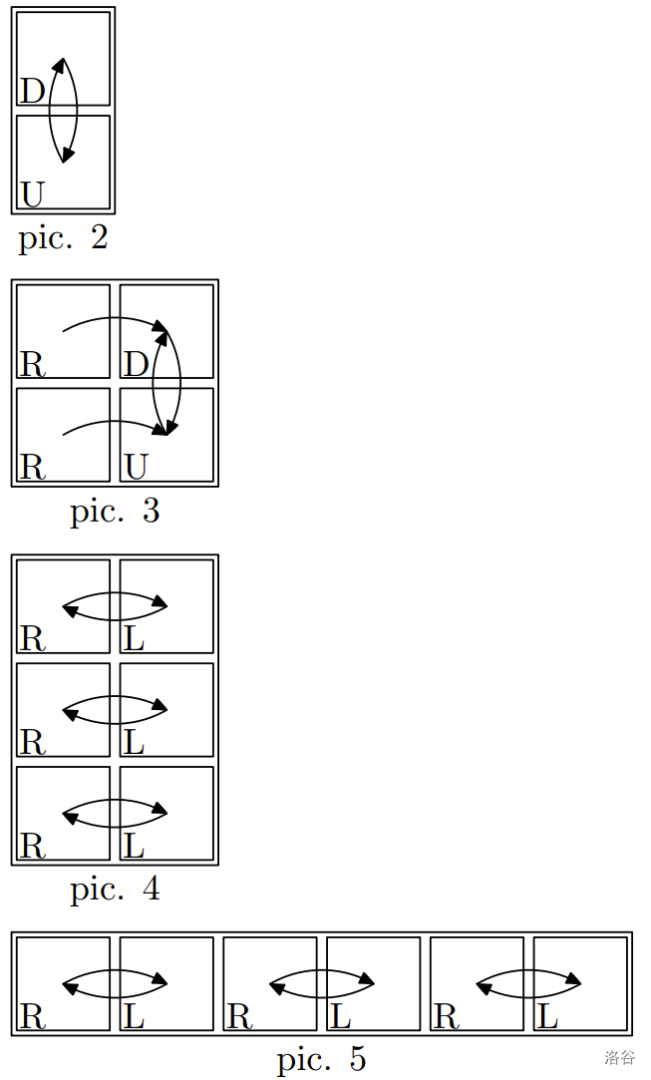
In the first example, there are two substrings that can constitute a description of an admissible map --- $\texttt{RDUL}$ as a matrix of size $2 \times 2$ (pic. 1) and $\texttt{DU}$ as a matrix of size $2 \times 1$ (pic. 2). In the second example, no substring can constitute a description of an admissible map. E.g. if we try to look at the string $\texttt{RDRU}$ as a matrix of size $2 \times 2$, we can find out that the resulting graph is not a set of cycles (pic. 3). In the third example, three substrings $\texttt{RL}$, two substrings $\texttt{RLRL}$ and one substring $\texttt{RLRLRL}$ can constitute an admissible map, some of them in multiple ways. E.g. here are two illustrations of substring $\texttt{RLRLRL}$ as matrices of size $3 \times 2$ (pic. 4) and $1 \times 6$ (pic. 5).