P12820 [NERC 2021] Global Warming

你正在开发一款新的电脑游戏。考虑三维空间中海洋中央的一座岛屿，其中 $z$ 轴垂直向上。海洋表面是水平面 $z = 0$。岛屿是一个特殊形态的多面体。 给定 $n$ 个点 $(x_i, y_i, z_i)$，这些点之间存在若干边。如果从上方观察岛屿或忽略每个点的 $z$ 坐标，这些点和边构成一个平面连通图。该平面图的每个内部面（除外部面外）都是非退化三角形。图的每条边至少属于一个内部面。所有位于平面图外部面边上的点 $z$ 坐标均为零，其他点的 $z$ 坐标可以是任意非负值。平面图的每个面对应多面体中具有相同顶点的面。 由于全球变暖，海平面上升并逐渐淹没岛屿。你的任务是为游戏计算不同的全球变暖情景。 在每个情景中，海平面上升到高度 $h$，此时海洋表面为平面 $z = h$。岛屿中**高度小于等于 $h$** 的部分被**淹没**，即使某些部分可能无法被海水触及（参见第二个样例的图示）。在情景中，玩家站在第 $p$ 个点上。你需要计算玩家所在岛屿部分的表面积，或者判定玩家所在位置已被淹没（即玩家已溺水）。 形式化地说，如果两个点位于岛屿表面，且玩家可以严格高于海平面的情况下在岛屿表面行走从一个点到达另一个点，则认为这两个点属于同一部分。注意，你需要计算岛屿表面的实际面积，而非其在水平面上的投影面积。

第一行包含一个整数 $n$ —— 点的数量（$1 \le n \le 10^5$）。 接下来的 $n$ 行，每行包含三个整数 $x_i$、$y_i$ 和 $z_i$ —— 第 $i$ 个点的坐标（$-10^6 \le x_i, y_i \le 10^6$；$0 \le z_i \le 10^6$）。 接下来一行包含一个整数 $m$ —— 平面图的内部面数量（$1 \le m \le 10^5$），也是岛屿多面体的面数量。 接下来的 $m$ 行，每行包含三个整数 $a_i$、$b_i$ 和 $c_i$ —— 第 $i$ 个内部面的三个顶点索引（$1 \le a_i, b_i, c_i \le n$）。 保证忽略 $z$ 坐标后，所得图是连通且平面的。除外部面外，所有面均为非退化三角形。所有位于平面图外部面边上的点 $z$ 坐标为零。 接下来一行包含一个整数 $q$ —— 需要计算的全球变暖情景数量（$1 \le q \le 10^5$）。 接下来的 $q$ 行，每行包含两个整数 $h_i$ 和 $p_i$ —— 海平面高度和玩家所在点的索引（$0 \le h_i \le 10^6$；$1 \le p_i \le n$）。

对于每个情景，输出一个实数 —— 玩家所在岛屿部分的表面积。如果玩家所在位置被淹没，输出 $-1$。 答案的绝对或相对误差不超过 $10^{-6}$ 即视为正确。

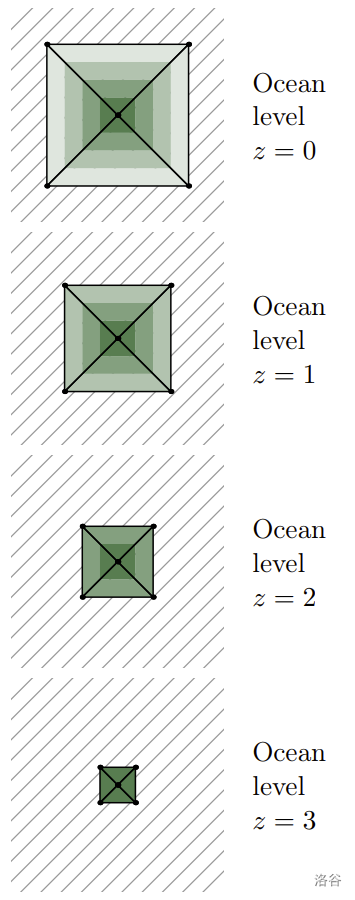
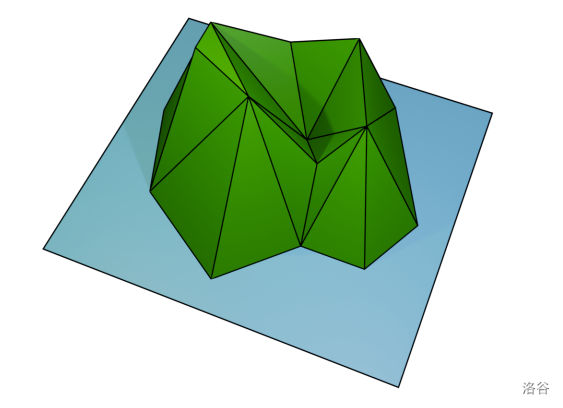
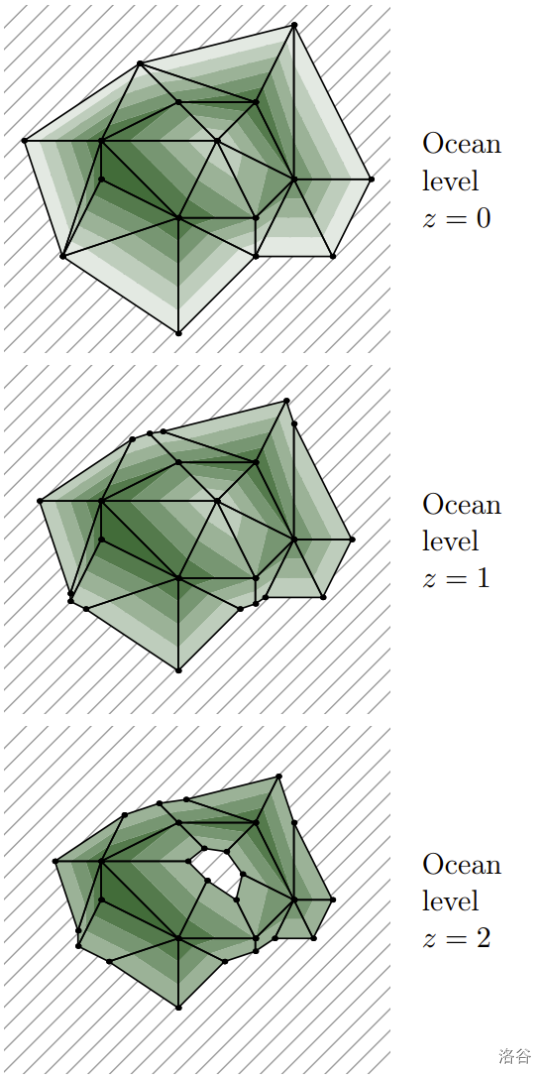
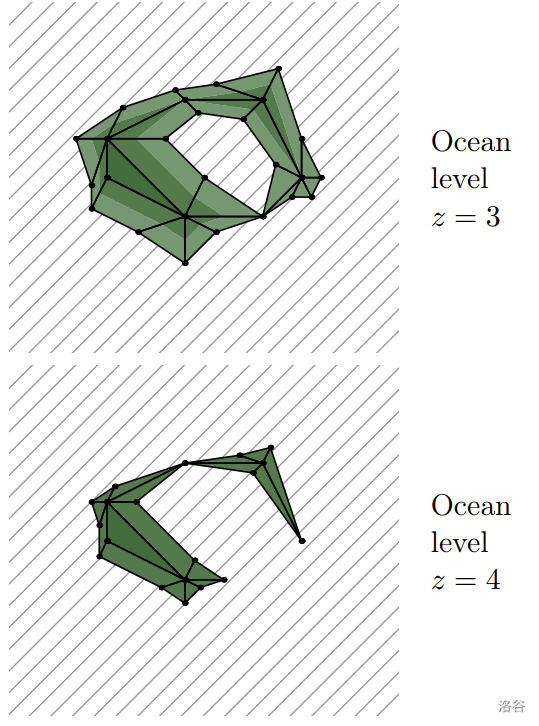
样例图示为岛屿的俯视图。淹没区域用阴影表示，岛屿用等高线绘制，颜色越深表示高度越高。 ### 样例 1  ### 样例 2 第二个样例中的岛屿形态如下：    翻译由 DeepSeek V3 完成