P1282 Dominoes

A domino consists of two squares, upper and lower. Each square has $1$ to $6$ pips. For a row of dominoes, let $S_1$ be the sum of pips in the upper squares and $S_2$ be the sum of pips in the lower squares. Their difference is $\left|S_1 - S_2\right|$. As shown in the figure, $S_1 = 6+1+1+1 = 9$, $S_2 = 1+5+3+2 = 11$, and $\left|S_1 - S_2\right| = 2$. Each domino can be rotated by $180°$ so that the upper and lower squares swap positions. Please compute the minimum number of rotations needed to make the difference between the two rows as small as possible.  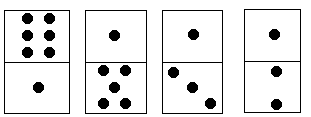For the example in the figure, rotating only the last domino by $180°$ makes the difference between the two rows equal to $0$.

The first line contains a positive integer $n$ ($1 \le n \le 1000$), the number of dominoes. Each of the next $n$ lines contains two positive integers $a$ and $b$ ($1 \le a, b \le 6$), representing the pips on the upper and lower squares of a domino.

Output a single line containing one integer: the minimum number of rotations.

Translated by ChatGPT 5