P12850 [NERC 2020 Online] Almost Balanced Tree

Consider a binary tree, each node has a weight equal to 1 or 2. The weight of a subtree is the sum of weights of all nodes in the subtree. The weight of an empty tree is 0. The binary tree is $\emph{almost balanced}$ if for each node, the difference of weights of its children subtrees is at most 1 (if one of the children is missing, its weight is considered to be 0). 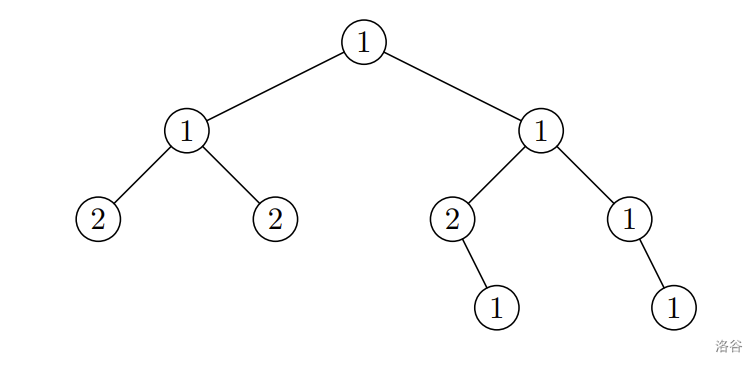Here is an example of an almost balanced binary tree:  Your task is to build any almost balanced binary tree with exactly $A$ nodes of weight 1 and $B$ nodes of weight 2, or to say that it is impossible.

The input contains two non-negative integers $A$ and $B$ ($1\le A+B\le 100\,000$).

Assign indices from 1 to $A+B$ to the nodes of your tree, node 1 should be the root of the tree. Output $A+B$ lines, one for each node. Each line should contain three integers --- the weight of the node, and the indices of the left and the right children of the node. If the corresponding child is missing, output 0 instead. If it is impossible to construct an almost balanced tree, output $-1$. If there are multiple possible answers, output any one of them.