P12856 [NERC 2020 Online] Geometrical Combinatorics

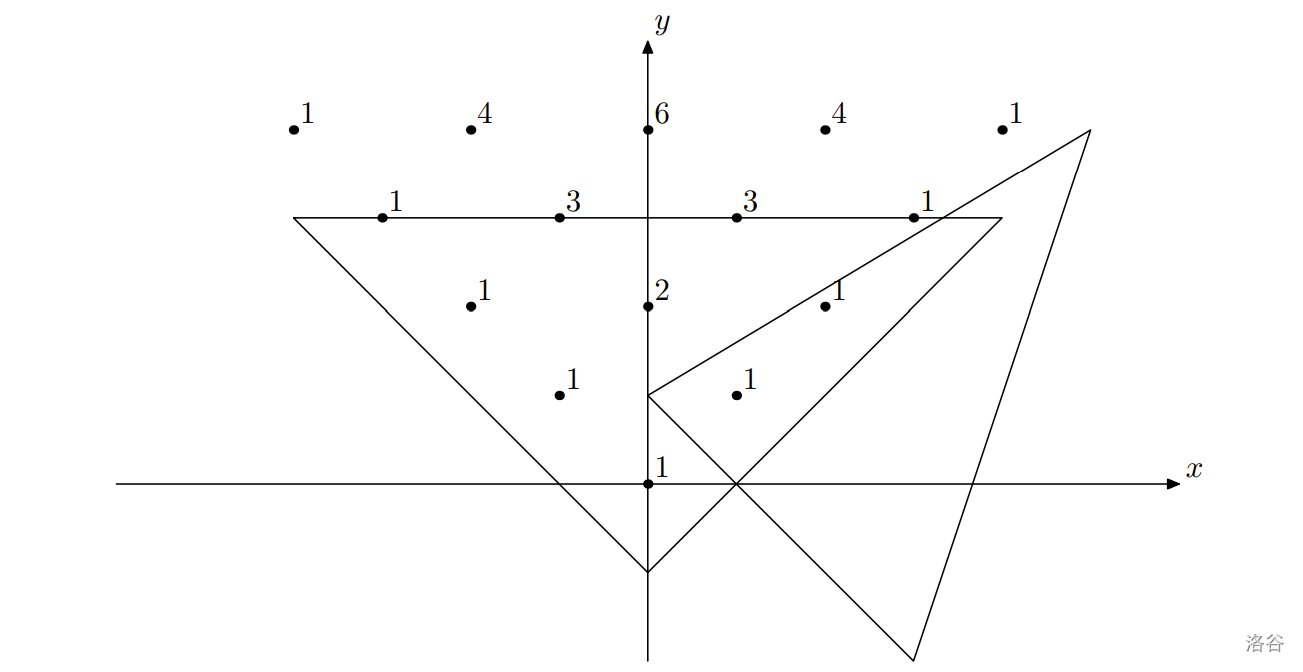
Grace 正在发展一种全新的几何组合学理论——研究组合对象的几何性质。 考虑平面上的两个三角形——**帕斯卡三角形**和**普通三角形**。帕斯卡三角形的根位于点 $(0, 0)$，两条边沿着上半平面象限的对角线延伸。正式定义如下： - 在点 $(i, i)$ 和 $(-i, i)$ 处标记数字 $1$； - 对于 $k$ 从 $1$ 到 $i-1$，在点 $(-i + 2k, i)$ 处的数字等于 $(-i + 2k + 1, i - 1)$ 和 $(-i + 2k - 1, i - 1)$ 两处数字之和。 普通三角形由顶点 $(x_A, y_A)$、$(x_B, y_B)$、$(x_C, y_C)$ 定义。  Grace 定义帕斯卡三角形与普通三角形的**交值**为：普通三角形内部或边界上所有帕斯卡三角形数字的总和。请你编写程序计算这一交值。

第一行输入整数 $t$（$1 \le t \le 5$）——测试用例数量。 接下来 $t$ 行，每行包含 6 个整数 $x_A, y_A, x_B, y_B, x_C, y_C$（$-10^6 \le x_A, y_A, x_B, y_B, x_C, y_C \le 10^6$），保证三点不共线。

对每个测试用例，输出交值对 $10^9+7$ 取模的结果。

翻译由 DeepSeek V3 完成