P12856 [NERC 2020 Online] Geometrical Combinatorics

Grace is developing a brand new theory of geometrical combinatorics --- a study about geometrical properties of combinatoric objects. Consider two triangles on plane --- a Pascal's triangle and an ordinary triangle. Pascal's triangle is drawn with it's root at point (0, 0), and two sides along diagonals of upper-halfplane quarters. Formally, there are 1's written in points $(i, i)$ and $(-i, i)$, and between them at point $(-i + 2 k, i)$ there is a number equal to the sum of numbers at $(-i + 2k + 1, i - 1)$ and at $(-i + 2k - 1, i - 1)$ for all $k$ from $1$ to $i - 1$. An ordinary triangle is drawn as just a triangle with vertices at $(x_A, y_A)$, $(x_B, y_B)$, $(x_C, y_C)$.  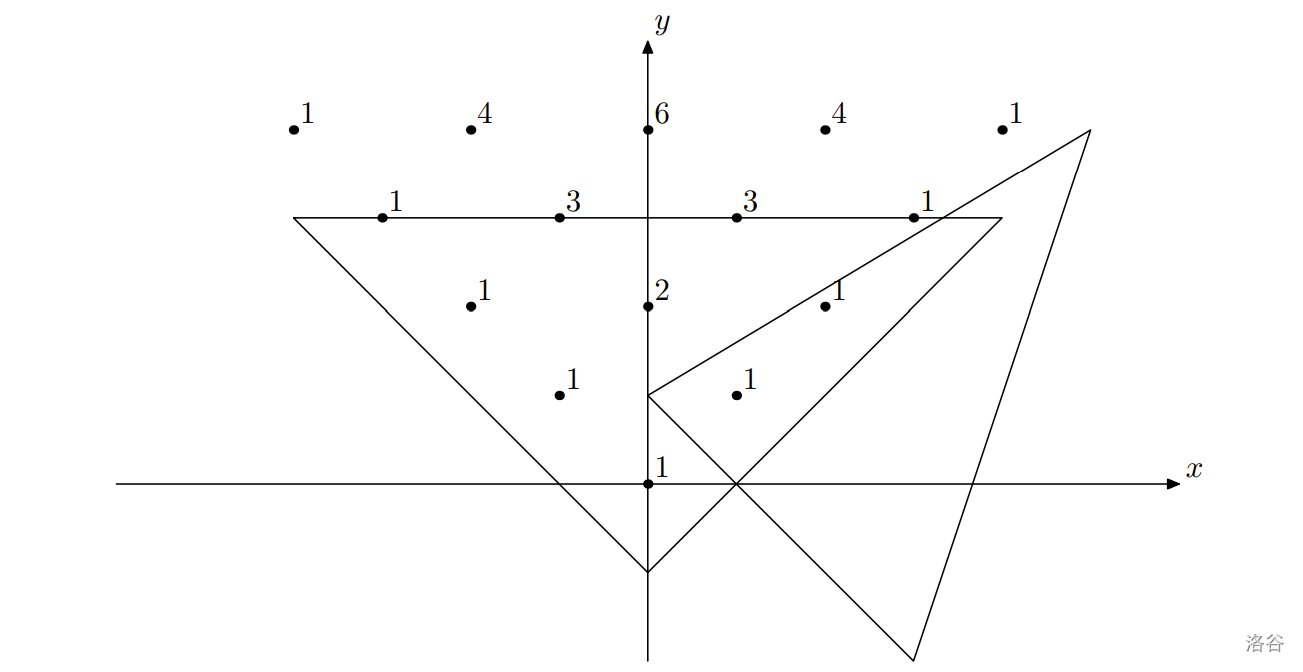Grace defines an $\emph{intersection value}$ of Pascal's triangle and an ordinary triangle as the sum of values of Pascal's triangle inside or on the border of the ordinary triangle. Can you develop a program that calculates this intersection value?

On the first line there is an integer $t$ ($1 \le t \le 5$) --- the number of tests to process. Each of the next $t$ lines contains 6 integers $x_A$, $y_A$, $x_B$, $y_B$, $x_C$, $y_C$ ($-10^6 \le x_A, y_A, x_B, y_B, x_C, y_C \le 10^6$). Three points in each test do not lie on a line.

For each test output an integer --- the intersection value modulo $10^9+7$.