P12859 [NERC 2020 Online] Jumping Cat

城市天际线由 $n$ 个整数 $d_1, d_2, \ldots, d_n$（$0 < d_1 < d_2 < \ldots < d_n$）和 $n$ 个整数 $h_1, h_2, \ldots, h_n$ 定义。 天际线表面由 $n$ 条水平线段组成，第 $i$ 条线段连接点 $(d_{i-1}, h_i)$ 和 $(d_i, h_i)$（其中 $d_0 = 0$）。每条线段代表一栋建筑的屋顶。 一只猫（体积极小可视为质点）需要从天际线最左端点 $(0, h_1)$ 移动到最右端点 $(d_n, h_n)$。为此，猫会执行一系列移动操作，每次操作有两种类型： 1. **行走**：从点 $(x_1, y_1)$ 移动到点 $(x_2, y_2)$。两点必须位于同一条表面线段上，即存在 $i$ 使得 $y_1 = y_2 = h_i$ 且 $d_{i-1} \le x_1, x_2 \le d_i$。行走轨迹为直线段。 2. **跳跃**：从点 $(x_1, y_1)$ 移动到点 $(x_2, y_2)$。两点必须位于不同表面线段上，且需满足： - 两点间距离不超过 $L$； - 连接两点的直线段不与任何建筑相交，即不存在线段上的点 $(x, y)$ 和整数 $i$ 使得 $d_{i-1} < x < d_i$ 且 $y < h_i$。 猫的轨迹长度为所有移动操作的长度之和。求从 $(0, h_1)$ 到 $(d_n, h_n)$ 的最短轨迹长度，若无法到达则输出 $-1$。

第一行包含两个整数 $n$ 和 $L$（$1 \le n \le 50$；$1 \le L \le 100$）。 第二行包含 $n$ 个整数 $d_1, d_2, \ldots, d_n$（$0 < d_1 < d_2 < \ldots < d_n \le 1000$）。 第三行包含 $n$ 个整数 $h_1, h_2, \ldots, h_n$（$1 \le h_i \le 100$；$h_i \ne h_{i+1}$）。

输出一个浮点数表示最短轨迹长度，若不可达则输出 $-1$。答案的绝对或相对误差不超过 $10^{-9}$ 即视为正确。

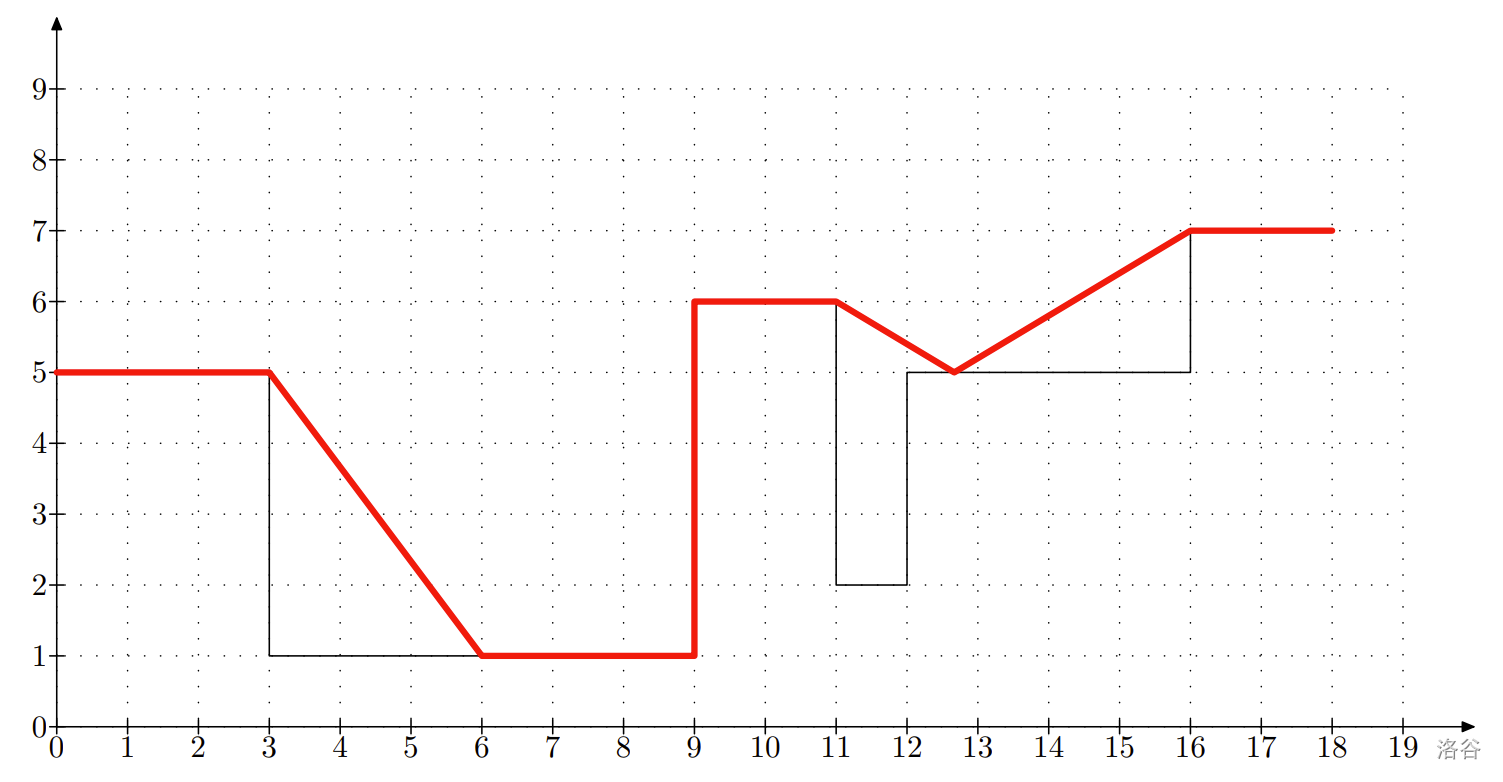
第一组样例的图示如下：  翻译由 DeepSeek V3 完成