P12867 [JOI Open 2025] 心灵感应 / Telepathy

译自 [JOI Open 2025](https://contests.ioi-jp.org/open-2025/index.html) T3「[Telepathy](https://www.luogu.com.cn/fe/api/problem/downloadAttachment/ipo36fvo)」/ 「[テレパシー](https://www.luogu.com.cn/fe/api/problem/downloadAttachment/axpo7zc2)」。 **这是一道通信题**。请使用 $\texttt{\textcolor{red}{C++\,20}}$ 提交。 **不要** $\texttt{\#include "telepathy.h"}$。

**这是一道通信题**。 Aitana 和 Bruno 在游玩 Bolivia 的一座国家公园。园内有 $N$ 个景点，$(N-1)$ 条道路，每条道路连接两个景点。可以通过道路从任意一个景点到达任意一个景点。 他们在游玩时走散了。此刻开始，他们必须同时抵达某个景点，在那里汇合。然而，身处亚马逊雨林深处，他俩无法互相通信。他们唯一可以依靠的是手头上的地图，地图刻画了公园的结构。他俩在自己的地图上给每个景点标号了 $0,1,\ldots,N-1$。**然而，Aitana 和 Bruno 的标号可能不同**。 为了汇合，Aitana 和 Bruno 现在开始移动。每一轮，他们同时做以下两件事之一：通过一条道路移动到相邻的景点，或者原地不动。 编程实现一个能够让 Aitana 和 Bruno 汇合的策略。本题中，如果在 $6d$ 轮内让他俩汇合，可以获得满分；这里，$d$ 是 Aitana 景点到 Bruno 景点最短路上的边数。**注意，如果他们在道路中间相遇，不算作汇合。** 本题单个测试点内有 $Q$ 组测试数据。 ### 形式化题意 我们形式化地描述题意。 国家公园的每个景点都分配了一个 $0\sim N-1$ 的标号，第 $j$（$0\le j\le N-2$）条道路连接标号为 $u_j,v_j$ 的景点。标号为 $i$（$0\le i\le N-1$）的景点在 Aitana 的地图上标号为 $p_i$，在 Bruno 的地图上标号 $q_i$。这里，$(p_0,p_1,\ldots,p_{N-1})$ 和 $(q_0,q_1,\ldots,q_{N-1})$ 是 $(0,1,\ldots,N-1)$ 的排列。 Aitana 知道，对于 $j=0,1,\ldots,N-2$，有一条连接标号 $A_j,B_j$ 的景点的道路，并且此时她位于标号为 $S$ 的景点。这里的「标号」指的是 Aitana 地图上的标号。从而，第 $j\, (0\le j\le N-2)$ 条路连接着标号 $p_{u_j},p_{v_j}$ 的景点，并且令 Aitana 现在所在的景点标号为 $s$，有 $S=p_s$。注意，道路不一定按顺序给出，也不一定是 $u_j,v_j$ 的顺序。类似地，Bruno 知道，对于 $j=0,1,\ldots,N-2$，有一条连接标号 $C_j,D_j$ 的景点的道路，并且此时她位于标号为 $T$ 的景点。这里的「标号」指的是 Bruno 地图上的标号。特别地，令 Bruno 现在所在的景点标号为 $t$，有 $T=q_t$。 根据已知信息，Aitana 和 Bruno 决定他们接下来 $10N$ 轮的动向。换言之，Aitana 选定标号序列 $x_0,x_1,\ldots,x_{10N}$，Bruno 选定标号序列 $y_0,y_1,\ldots,y_{10N}$，表示他们各自的动向。以下条件必须满足： - $x_0=S$，$\forall 1\le k\le 10N$，要么 $x_k=x_{k-1}$，要么（在 Aitana 的地图中）标号 $x_k,x_{k-1}$ 的节点有道路连接。 - $y_0=T$，$\forall 1\le k\le 10N$，要么 $y_k=y_{k-1}$，要么（在 Bruno 的地图中）标号 $y_k,y_{k-1}$ 的节点有道路连接。 Aitana 与 Bruno 汇合时的轮数 $k^*$ 指最小的满足（Aitana 的地图中）标号 $x_k$ 的景点与（Bruno 的地图中）标号 $y_k$ 的景点代表着同一个景点的 $k$。获得满分，当且仅当 $k^*\le 6d$。 ### 实现细节 **这是一道通信题**。你不应该，也不需要定义 `main` 函数。 **不要** $\texttt{\#include "telepathy.h"}$。 你应该定义以下的函数： ```cpp vector Aitana(int N, vector A, vector B, int S, int subtask); ``` 该函数实现了 Aitana 的策略。每组测试数据中该函数被调用恰好一次，所以该函数一共会被调用 $Q$ 次。 - $\texttt{N}$ 指国家公园的景点数 $N$。 - $\texttt{A},\texttt{B}$ 均为长度 $N-2$ 的数组，$\forall 0\le j\le N-2$，$\texttt{A[j]},\texttt{B[j]}$ 是一条道路连接着的两个景点的标号 $A_j,B_j$。 - $\texttt{S}$ 为 Aitana 当前所在景点的标号。 - $\texttt{subtask}$ 指该测试点所在的子任务编号，只能为 $1,2,3$ 之一。 - 返回一个数组 $[x_0,x_1,\ldots,x_{10N}]$，描述 Aitana 的动向。 - 返回的数组长度必须为 $10N+1$，否则会被判为 $\texttt{Wrong Answer\,[1]}$。 - 对于任意 $k\, (0\le k\le 10N)$，必须有 $0\le x_k\le N-1$，否则会被判为 $\texttt{Wrong Answer\,[2]}$。 - 必须有 $x_0=S$，否则会被判为 $\texttt{Wrong Answer\,[3]}$。 - 对于任意 $k\, (1\le k\le 10N)$，要么 $x_k=x_{k-1}$，要么标号 $x_k,x_{k-1}$ 的景点有道路连接。否则会被判为 $\texttt{Wrong Answer\,[4]}$。 以上的「标号」指的是 Aitana 地图上的标号。 ```cpp vector Bruno(int N, vector C, vector D, int T, int subtask); ``` 该函数实现了 Bruno 的策略。每组测试数据中该函数在调用 `Aitana` 后被调用恰好一次，所以该函数一共会被调用 $Q$ 次。 - $\texttt{N}$ 指国家公园的景点数 $N$。 - $\texttt{C},\texttt{D}$ 均为长度 $N-2$ 的数组，$\forall 0\le j\le N-2$，$\texttt{C[j]},\texttt{D[j]}$ 是一条道路连接着的两个景点的标号 $C_j,D_j$。 - $\texttt{T}$ 为 Bruno 当前所在景点的标号。 - $\texttt{subtask}$ 指该测试点所在的子任务编号，只能为 $1,2,3$ 之一。 - 返回一个数组 $[y_0,y_1,\ldots,y_{10N}]$，描述 Bruno 的动向。 - 返回的数组长度必须为 $10N+1$，否则会被判为 $\texttt{Wrong Answer\,[5]}$。 - 对于任意 $k\, (0\le k\le 10N)$，必须有 $0\le y_k\le N-1$，否则会被判为 $\texttt{Wrong Answer\,[6]}$。 - 必须有 $y_0=T$，否则会被判为 $\texttt{Wrong Answer\,[7]}$。 - 对于任意 $k\, (1\le k\le 10N)$，要么 $y_k=y_{k-1}$，要么标号 $y_k,y_{k-1}$ 的景点有道路连接。否则会被判为 $\texttt{Wrong Answer\,[8]}$。 以上的「标号」指的是 Bruno 地图上的标号。 如果在 $10N$ 轮内 Aitana 和 Bruno 没有汇合，换句话说，$\forall 0\le k\le 10N$，（Aitana 的地图中）标号 $x_k$ 的景点与（Bruno 的地图中）标号 $y_k$ 的景点均为不同的景点，你的程序会被判为 $\texttt{Wrong Answer\,[9]}$。 ### 重要说明 - 你可以在程序中定义其他函数或使用全局变量。在实际评测时，你的程序将会以两个不同的进程（Aitana,Bruno）运行，这两个进程无法共享全局变量。 - 你的程序不得使用标准输出输出，禁止以任何方式与任何文件交互。你可以输出调试信息到标准错误流。 ### 编译运行 你可以在「附件」中下载附件压缩包，压缩包中包含 Sample Grader 和本题的示例文件。 Sample Grader 是文件 $\texttt{grader.cpp}$。为测试程序，将 $\texttt{grader.cpp},\texttt{telepathy.cpp},\texttt{telepathy.h}$ 置于同一目录下，用以下命令来编译： ```bash g++ -std=gnu++20 -O2 -o grader grader.cpp telepathy.cpp ``` 此外，你也可以运行压缩包中的 $\texttt{compile.sh}$ 来编译： ```bash ./complie.sh ``` 若编译成功，会生成名为 $\texttt{grader}$ 的可执行文件。 注意，实际测评时使用的 Grader 与 Sample Grader 不同。Sample Grader 以单进程方式执行，从标准输入流读入数据并将结果输出至标准输出流。

Sample Grader 从标准输入流读入以下格式的数据（这里，测试数据编号 $0\sim Q-1$，$\mathrm{subtask}$ 指子任务编号）： > $\mathrm{subtask}$\ > $Q$\ > (第 $0$ 组数据的内容)\ > (第 $1$ 组数据的内容)\ > $\vdots$\ > (第 $(Q-1)$ 组数据的内容) 每组数据格式如下： > $N$\ > $u_0$ $v_0$\ > $u_1$ $v_1$\ > $\vdots$\ > $u_{n-2}$ $v_{n-2}$\ > $p_0$ $p_1$ $\ldots$ $p_{N-1}$\ > $q_0$ $q_1$ $\ldots$ $q_{N-1}$\ > $s$ $t$ 关于各变量的含义，请阅读「形式化题意」部分。**注意没有直接输入 Aitana 地图和 Bruno 地图的信息。** 将道路打乱的方式由伪随机数决定，伪随机数的结果在各次运行中均相同。如果想要更换随机数种子，将随机数种子作为第一个参数运行 Sample Grader： ```bash ./grader 20250615 ```

Sample Grader 输出 $Q$ 行到标准输出流，依次表示每组测试数据的信息： - 若该组数据正确，依次输出汇合轮数 $k^{*}$ 和 $d$（Aitana 当前所在景点与 Bruno 当前所在景点的最短路上的边数），例如 $\texttt{Case \#0: Accepted 5 2}$。 - 否则，输出错误类型，如 $\texttt{Case \#0: Wrong Answer [1]}$。

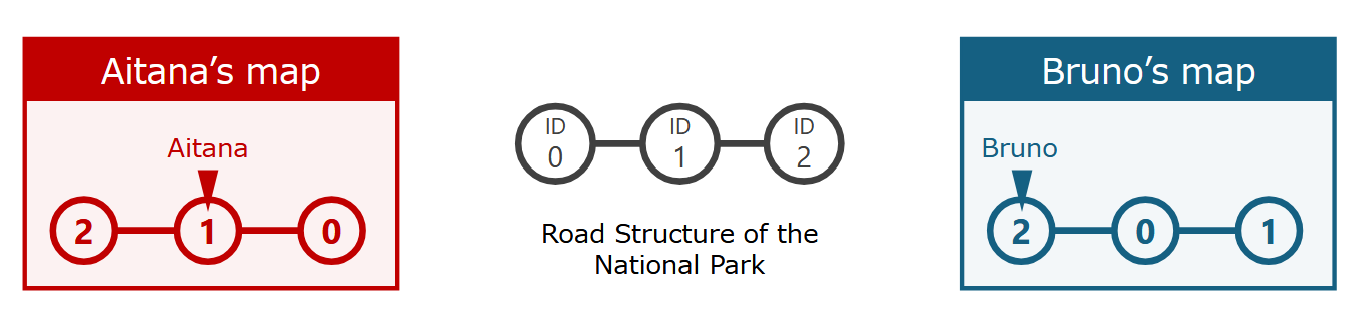
### 注意事项 实际评测时，输入未必在程序执行前就确定了，有可能会根据 `Aitana` 和 `Bruno` 的返回值确定。 ### 样例解释 返回值中，若干部分被省略了，实际上每个返回值都是长度为 $31$ 的数组。 调用 `Aitana`：$\texttt{Aitana(3,[0,1],[1,2],1,2)}$，返回 $\texttt{[1,0,0,1,2,...,2]}$。 调用 `Bruno`：$\texttt{Bruno(3,[1,0],[2,0],2,2)}$，返回 $\texttt{[2,2,0,0,1,...,1]}$。 该样例中，国家公园的结构以及 Aitana、Bruno 地图上的信息如图所示：  Aitana 的动向是：每一轮中，她分别在（她地图中）标号 $1,0,0,1,2,\ldots,2$ 的景点。Bruno 的动向是：每一轮中，他分别在（他地图中）标号 $2,2,0,0,1,\ldots,1$ 的景点。他们第 $3$ 轮结束时汇合。此时，Aitana 在（她地图中）标号 $1$ 的景点，Bruno 在（他地图中）标号 $0$ 的景点，这两个实际上是同一个景点。 ### 数据范围 本题中，单组数据中至多有 $201$ 个测试点（即 $1\le Q\le 201$）。每个测试点满足以下的限制： - $2\le N\le 200$； - $(p_0,p_1,\ldots,p_{N-1})$ 是 $(0,1,\ldots,N-1)$ 的排列； - $(q_0,q_1,\ldots,q_{N-1})$ 是 $(0,1,\ldots,N-1)$ 的排列； - $0\le u_j\le N-1\, (0\le j\le N-2)$； - $0\le v_j\le N-1\, (0\le j\le N-2)$； - 从任意景点，可通过道路移动到任意景点； - $0\le s\le N-1$； - $0\le t\le N-1$； - $s\neq t$。 ### 子任务 - $\text{Subtask 1 (40 pts)}$：$(p_0,p_1,\ldots,p_{N-1})$=$(q_0,q_1,\ldots,q_{N-1})=(0,1,\ldots,N-1)$； - $\text{Subtask 2 (40 pts)}$：$u_j=j,v_j=j+1$（$0\le j\le N-2$）； - $\text{Subtask 3 (20 pts)}$：无额外限制。 ### 计分方式 令 $k^{*}$ 表示 Aitana 和 Bruno 汇合的轮数，$d$ 表示 Aitana 当前所在景点与 Bruno 当前所在景点的最短路上的边数。令 $\alpha$ 表示该子任务重 $\frac{k^*}{d}$ 的最大值。 如果该子任务中你的程序被判为错误，得零分。否则，按照以下方式得分（若同时满足多个条件，则取最高的分数）： - 若任意数据都有 $k^*\le 10N$，得 $15\%$ 的分。 - 若任意数据都有 $k^*\le \max(10d,N)$，得 $25\%$ 的分。 - 若任意数据都有 $k^*\le 10d$： - 若 $9\lt \alpha\le 10$，得 $40\%$ 的分； - 若 $0\lt \alpha\le 9$，得 $\lfloor 100-20(\alpha-6)\rfloor \%$ 的分； - 若 $\alpha\le 6$，得 $100\%$ 的分。