P1288 Number Picking Game II

There is a number-picking game. Initially, you are given a ring; each edge on the ring has a non-negative integer on it. Among these integers, at least one is $0$. Then, a coin is placed on a node of the ring. Starting from this node, two players take turns according to the following rules: 1. Choose one of the two edges adjacent to the coin (left or right), and its number must be non-zero. 2. Decrease the number on that edge to any non-negative integer (it must strictly decrease). 3. Move the coin to the other endpoint of that edge. If it is a player's turn and the numbers on both edges adjacent to the coin are $0$, then that player loses. As shown below is a sequence of moves between Alice and Bob (the black node marks the coin's position).  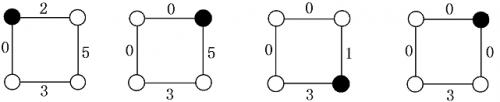The results of the panels are: - $\text{A}$: Alice to move. - $\text{B}$: Bob to move. - $\text{C}$: Alice to move. - $\text{D}$: Bob to move. In $\text{D}$, when it is Bob's turn, both adjacent edges have number $0$, so Alice wins. Your task is to determine, given the ring, the edge values, and the starting node (the coin's position), whether the first player has a forced winning strategy.

The first line contains an integer $N$ $(N \leq 20)$, the number of nodes on the ring. The second line contains $N$ integers, each not exceeding $30$, giving the values on the $N$ edges in order. The coin initially sits on the node between the first edge and the last edge.

Output a single line. If there exists a winning strategy, output ```YES```, otherwise output ```NO```.

Translated by ChatGPT 5