P12896 [POI 2019/2020 R2] 四叉树 Drzewo czwórkowe

翻译来自于 [LibreOJ](https://loj.ac/p/4845)。

**题目译自 [XXVII Olimpiada Informatyczna – II etap](https://sio2.mimuw.edu.pl/c/oi27-2/dashboard/) [Drzewo czwórkowe](https://szkopul.edu.pl/problemset/problem/GcP-wwgKv1HiCzuFRKE6n7-U/statement/)** 给定一个尺寸为 $2^{m} \times 2^{m}$ 的方形位图，每个像素要么是白色，要么是黑色。这样的位图可以用四叉树进行压缩表示。如果位图中的所有像素都是白色，四叉树只有一个节点，标记为 $0$；如果所有像素都是黑色，四叉树也只有一个节点，标记为 $1$；否则，四叉树的根节点标记为 $4$，并拥有四个子树，分别对应位图的四个象限（大小为 $2^{m-1} \times 2^{m-1}$），顺序为左上、右上、左下和右下。四叉树可以用一个由字符 `0`、`1` 和 `4` 组成的字符串来描述：树的描述从根节点的标记开始，后面依次是各个子树的描述。下图展示了一个 $m=3$ 的示例位图及其对应的四叉树，其描述字符串为 `404004111014001410011`。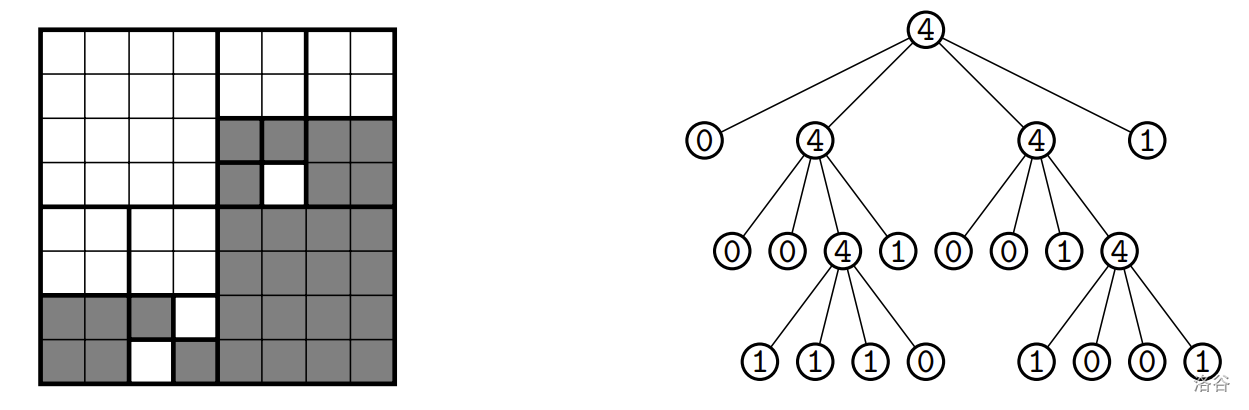  我们将**黑色联通块**定义为相互邻接的最大黑色像素集合（像素之间如果共享边则视为邻接）。对于给定的描述位图的字符串，计算位图中的黑色联通块数量以及最大黑色联通块的大小。在上述示例中，有两个黑色联通块，面积分别为 $24$ 和 $5$。 正式来说，黑色联通块是指黑色像素的集合，其中任意两个像素可以通过一系列黑色像素连接起来，每两个连续的像素共享边。黑色联通块被称为最大黑色联通块，当且仅当无法通过添加任何其他黑色像素来扩大它，同时仍保持为黑色联通块。在本题中，我们只考虑最大黑色联通块。

输入的第一行包含一个整数 $m$ $(m \geq 0)$，表示位图的大小。第二行包含一个非空的字符串，由字符 `0`、`1` 和 `4` 组成，用于编码位图。输入保证是合法的，特别是四叉树的高度（即从根节点到最深处节点的路径上的边数）不超过 $m$。位图中至少包含一个黑色像素。

你的程序应输出两行内容： 第一行包含一个整数，表示位图中的黑色联通块数量。 第二行包含一个整数，表示最大黑色联通块的大小。由于这个数字可能非常大，需输出其对 $10^{9}+7$ 取模的结果。

**附加样例** 1. 该样例满足 $m=3$，位图的四个角各有一个 $2 \times 2$ 的黑色方块，因此包含 $4$ 个大小为 $4$ 的黑色联通块； 2. 该样例满足 $m=9$，位图被涂成棋盘格样式，因此包含 $\left(2^{9}\right)^{2} / 2 = 2^{17}$ 个大小为 $1$ 的黑色联通块； 3. 该样例满足 $m=16$，位图全为黑色，因此包含 $1$ 个大小为 $\left(2^{16}\right)^{2} = 2^{32}$ 的黑色联通块。 详细子任务附加限制及分值如下表所示。 如果你的程序只正确输出了两行中的一行，可以获得该测试点 $50\%$ 的分数。但在这种情况下，仍然需要输出两行，每行包含一个 $0$ 到 $10^{9}+6$ 之间的整数。 | 子任务 | 附加限制 | 分值 | | :---: | :--: | :---: | | $1$ | $m \leq 10$ | $24$ | | $2$ | $m, n \leq 1000$ | $36$ | | $3$ | $m, n \leq 10^{6}$ | $32$ | | $4$ | $m \leq 10^{9}, n \leq 10^{6}$ | $8$ |