P12904 [NERC 2020] Equilibrium Point /\/\

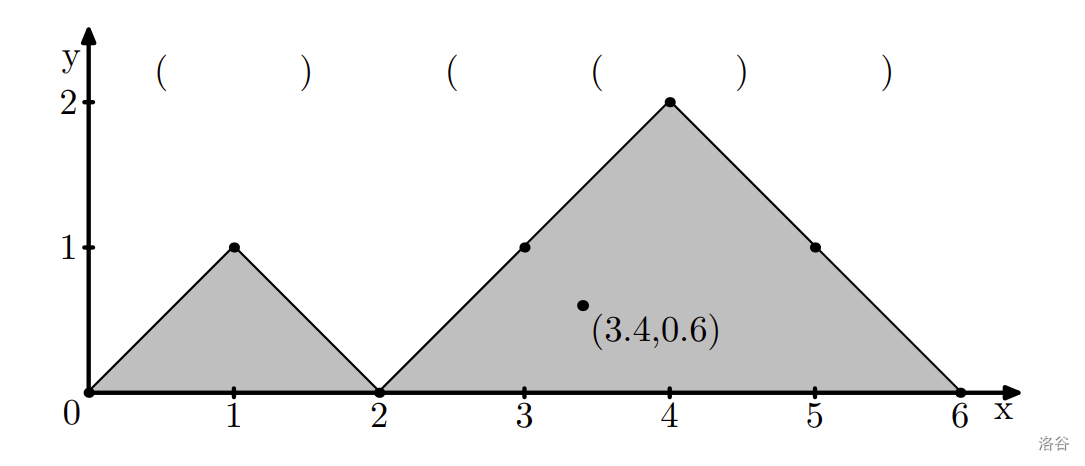
考虑一个由单种括号$\tt{(}$ 和 $\tt{)}$ 组成的平衡括号序列 $s$。 这种序列有一种常见的几何表示方法。从点 $(0, 0)$ 出发，根据每个括号类型绘制折线：遇到开括号 $\tt{(}$ 时沿向量 $(1, 1)$ 移动，遇到闭括号 $\tt{)}$ 时沿向量 $(1, -1)$ 移动。  考虑这条曲线与直线 $y=0$ 之间的区域。这个区域由若干多边形组成，其质心位于某个点 $(x, y)$。注意质心可能位于该区域之外。 现在你需要解决一个逆向问题：给定长度 $n$ 和一个点 $(x, y)$，找出任意一个长度为 $n$ 的平衡括号序列，使得其几何表示的质心位于 $(x, y)$。

第一行包含三个数字 $n$、$x$ 和 $y$（$n$ 为偶数，$2 \le n \le 36$；$0 < x, y < n$）—— 目标序列的长度和期望质心的坐标。 题目保证存在某个长度为 $n$ 的平衡括号序列，其几何表示的质心与 $(x, y)$ 的欧几里得距离误差不超过 $10^{-9}$。

输出一个由 $\tt{(}$ 和 $\tt{)}$ 组成的长度为 $n$ 的平衡括号序列，其几何表示的质心与点 $(x, y)$ 的欧几里得距离误差不超过 $10^{-7}$。

翻译由 DeepSeek V3 完成