P12905 [NERC 2020] Fiber Shape

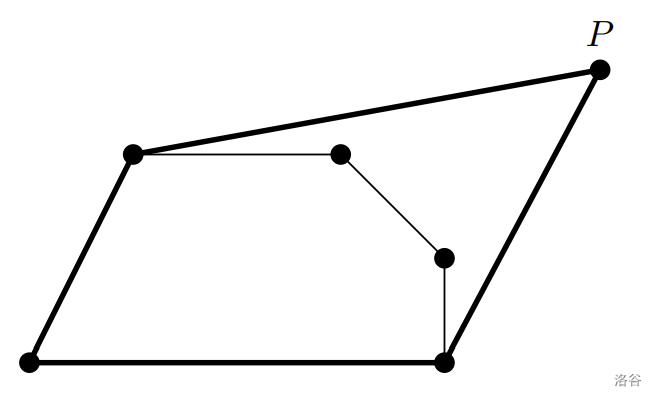
想象一块钉有 $n$ 个钉子的木板，第 $i$ 个钉子的位置为 $(x_i, y_i)$。为简化问题，我们限定这些钉子位于一个凸多边形的顶点上。 然后取一根长度为 $l$ 的不可伸缩细绳，将其绕过所有钉子。将铅笔置于细绳内侧，尝试向各个方向拉紧细绳并绘制出围绕钉子的曲线。下图展示了细绳绕钉并被铅笔（点 $P$）拉紧的示例。  你的任务是计算该曲线所围成的区域面积。正式地，对于给定凸多边形 $S$ 和长度 $l$，我们定义 **纤维形状** $F(S, l)$ 为满足以下条件的点 $t$ 的集合：$S \cup \{t\}$ 的凸包周长不超过 $l$。请计算 $F(S, l)$ 的面积。

第一行包含两个整数 $n$ 和 $l$（$3 \le n \le 10^4$；$1 \le l \le 8 \cdot 10^5$）—— 多边形 $S$ 的顶点数和细绳长度。接下来 $n$ 行每行包含两个整数 $x_i$ 和 $y_i$（$-10^5 \le x_i, y_i \le 10^5$）—— 按逆时针顺序给出的多边形顶点坐标。多边形的所有内角严格小于 $\pi$。长度 $l$ 至少比多边形周长大 $10^{-3}$。

输出一个浮点数——纤维形状 $F(S, l)$ 的面积。若答案的绝对或相对误差不超过 $10^{-6}$ 即视为正确。

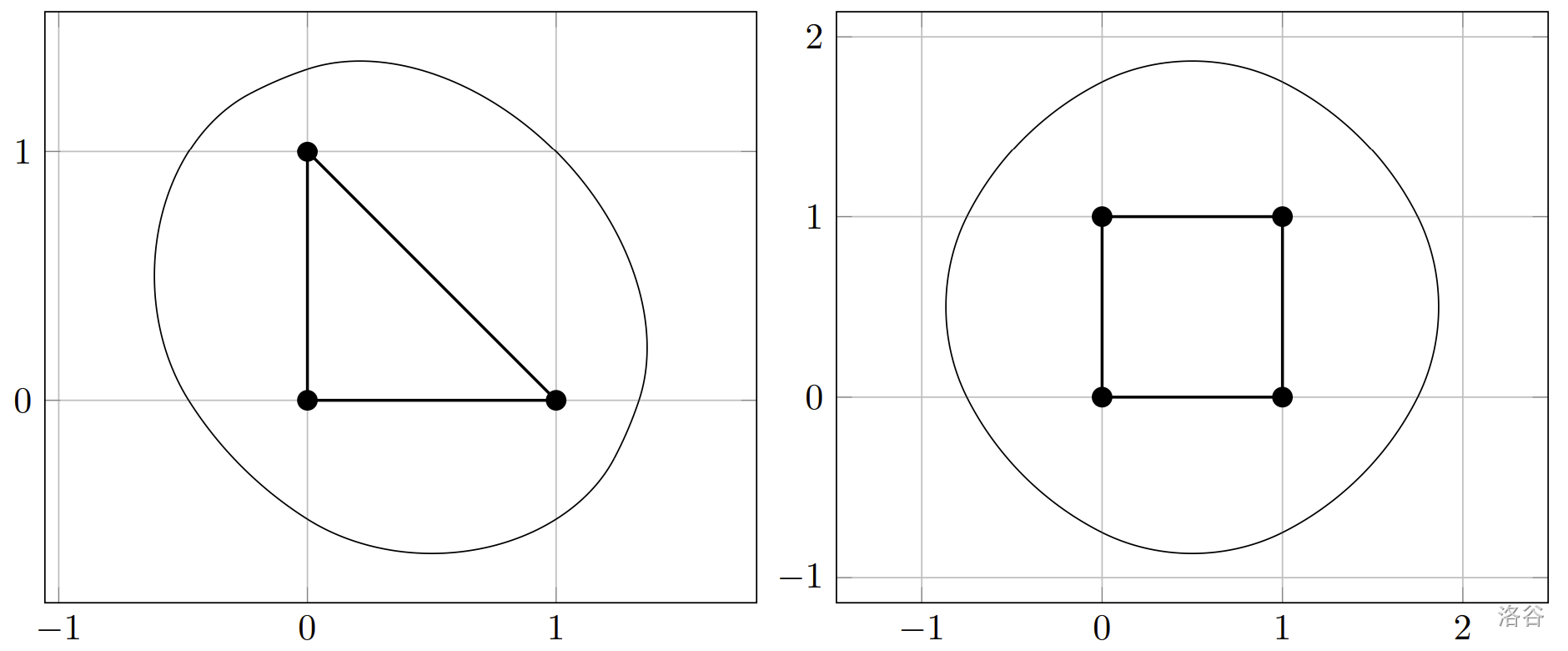
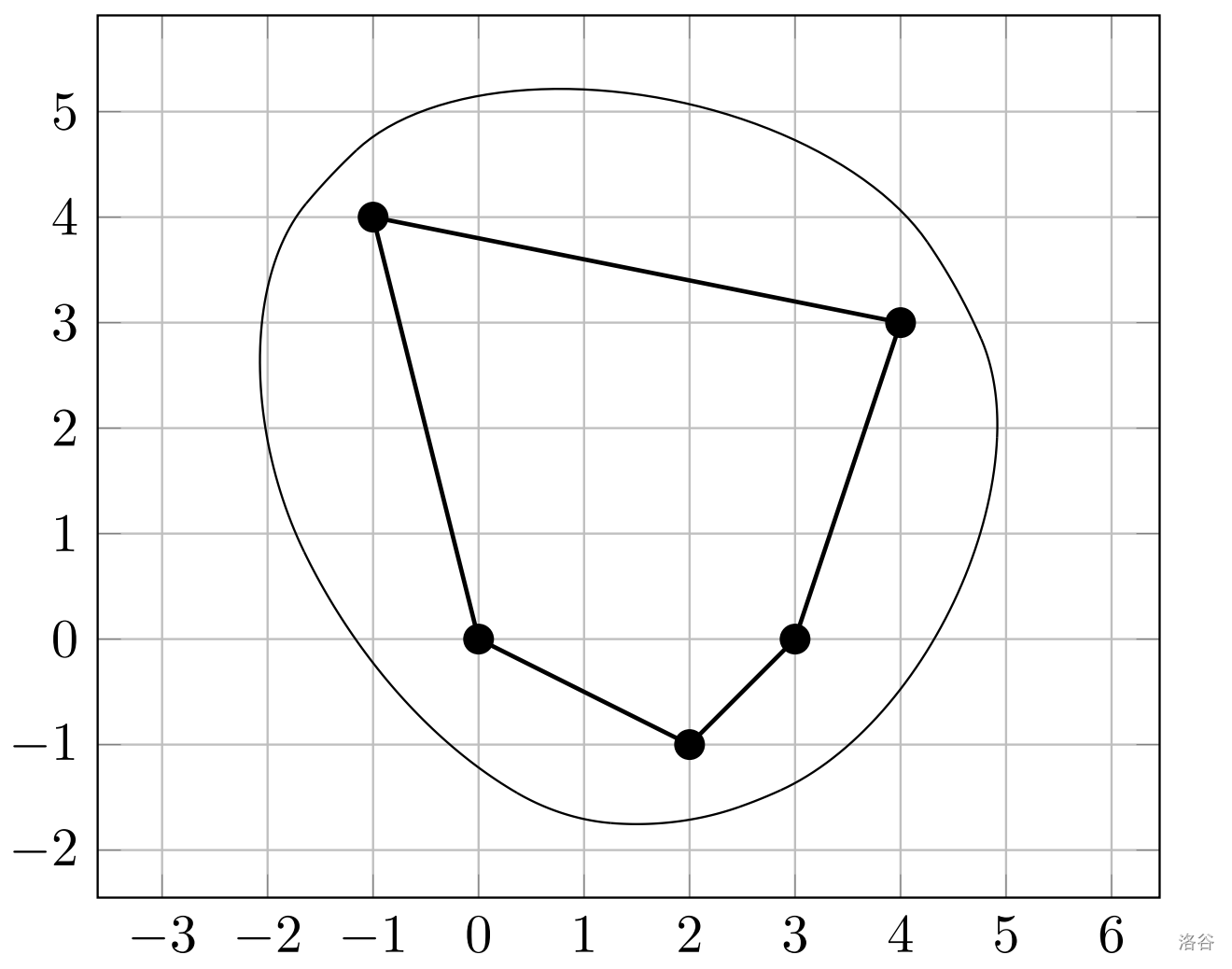
下图展示了样例测试的示意图。   翻译由 DeepSeek V3 完成