P12934 [NERC 2019] Apprentice Learning Trajectory

Abigail 是一名学徒，正在学习成为一名铁匠。她希望规划自己的学习轨迹，并在成为著名专家的道路上尽可能多地锻造剑。 共有 $n$ 位大师愿意收她为徒。第 $i$ 位大师将在第 $a_i$ 分钟开始工作，并在第 $b_i$ 分钟结束工作，总共工作 $b_i - a_i$ 分钟。在这段时间内，Abigail 可以在这位大师的铁匠铺中工作。她可以多次进入和离开铁匠铺，并在每次到达时锻造一把或多把剑。然而，为了在第 $i$ 位大师的指导下锻造一把剑，她必须连续工作 $t_i$ 分钟。她不能留下未完成的剑，并在下次到达铁匠铺时继续锻造。 请帮助 Abigail 制定一个最优计划，并计算她在 $n$ 位大师的指导下可以锻造的剑的最大数量。

第一行包含一个整数 $n$（$1 \le n \le 200\,000$）—— 大师的数量。 接下来的 $n$ 行，每行包含三个整数 $a_i$, $b_i$, $t_i$（$1 \le a_i < a_i + t_i \le b_i \le 10^{18}$）—— 大师工作的开始和结束时间，以及在其铁匠铺中锻造一把剑所需的时间。

输出 Abigail 使用最优学习轨迹可以锻造的剑的最大数量。

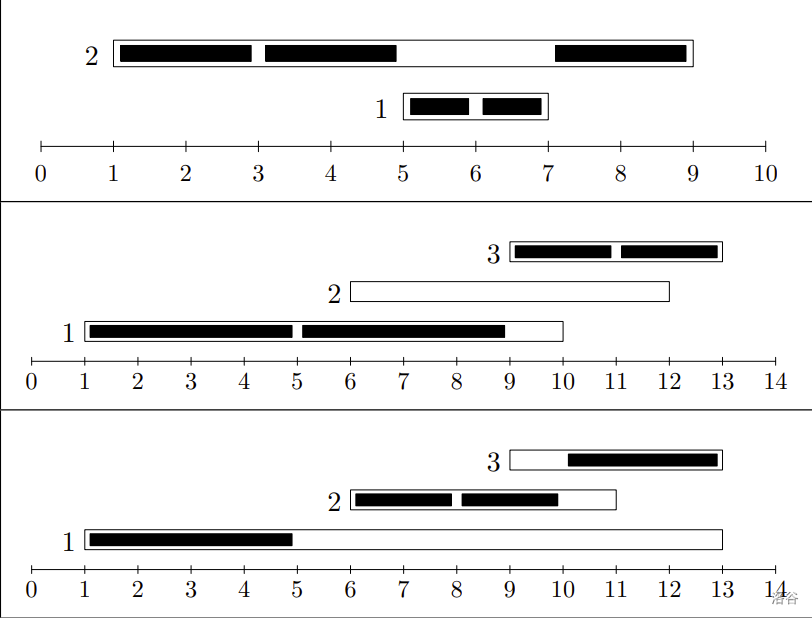
 翻译由 DeepSeek V3 完成