P12958 [GCJ Farewell Round #3] Evolutionary Algorithms

Ada 正在为学校的科学项目工作。她研究生物进化，并希望比较不同物种在解决编程竞赛问题时的表现。 共有 $\mathbf{N}$ 个物种，编号为 1 到 $\mathbf{N}$。物种 1 没有直接祖先，其他每个物种都有且仅有一个直接祖先。物种 $x$ 的（直接或间接）祖先是指从 $x$ 出发，通过一次或多次向上追溯直接祖先能到达的任何其他物种 $y$。因此，物种 1 是所有其他物种的（直接或间接）祖先。 通过复杂的遗传模拟，她计算了每个物种在特定编程竞赛中的平均得分 $\mathbf{S}_i$（$i$ 为物种编号）。 Ada 希望在她的展示中呈现一些有趣的三元组。一个有趣的三元组定义为满足以下条件的有序三元组 $(a, b, c)$（$a, b, c$ 为不同物种）： 1. 物种 $b$ 是物种 $a$ 的（直接或间接）祖先。 2. 物种 $b$ **不是**物种 $c$ 的（直接或间接）祖先。 3. 物种 $b$ 的平均得分严格大于 $\mathbf{K}$ 倍 $\max(\mathbf{S}_a, \mathbf{S}_c)$，即 $\mathbf{S}_b \geq \mathbf{K} \times \max(\mathbf{S}_a, \mathbf{S}_c) + 1$。 给定物种得分和祖先关系，编写程序计算所有满足条件的有趣三元组数量。

输入第一行包含测试用例数量 $\mathbf{T}$。每个测试用例包含三行： 1. 两个整数 $\mathbf{N}$（物种数）和 $\mathbf{K}$（判定系数）。 2. $\mathbf{N}$ 个整数 $\mathbf{S}_1, \mathbf{S}_2, \ldots, \mathbf{S}_\mathbf{N}$，表示各物种的平均得分。 3. $\mathbf{N} - 1$ 个整数 $\mathbf{P}_2, \mathbf{P}_3, \ldots, \mathbf{P}_\mathbf{N}$，表示物种 $i$ 的直接祖先为 $\mathbf{P}_i$。

对每个测试用例，输出一行 `Case #x: y`，其中 $x$ 为测试用例编号（从 1 开始），$y$ 为有趣三元组的总数。

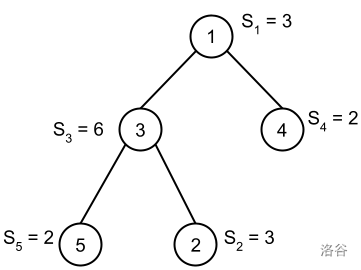
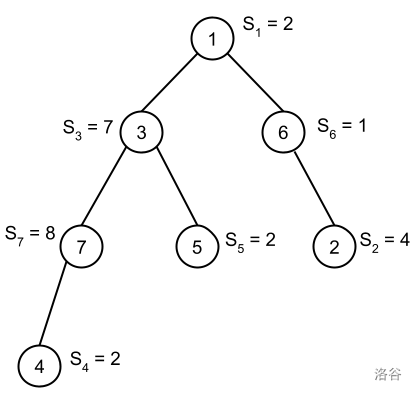
**样例解释**  在样例 #1 中，唯一满足条件的三元组是 $(5, 3, 4)$。验证如下： 1. 物种 3 是物种 5 的祖先。 2. 物种 3 不是物种 4 的祖先。 3. $\mathbf{S}_3 = 6 \geq 2 \times \max(2, 2) + 1 = 5$（设 $\mathbf{K} = 2$）。  在样例 #2 中，共有 7 个有趣三元组： - $(4, 3, 1)$ - $(4, 3, 6)$ - $(4, 7, 1)$ - $(4, 7, 5)$ - $(4, 7, 6)$ - $(5, 3, 1)$ - $(5, 3, 6)$ **限制条件** - $1 \leq \mathbf{T} \leq 100$。 - $1 \leq \mathbf{K} \leq 10^9$。 - $1 \leq \mathbf{S}_i \leq 10^9$。 - 物种 1 是所有其他物种的祖先。 **测试集 1（7 分，可见判定）** - $3 \leq \mathbf{N} \leq 1000$。 **测试集 2（16 分，隐藏判定）** - 最多 30 个测试用例：$3 \leq \mathbf{N} \leq 2 \times 10^5$。 - 其余测试用例：$3 \leq \mathbf{N} \leq 1000$。 翻译由 DeepSeek V3 完成