P12961 [GCJ Farewell Round #4] Indispensable Overpass

Ekiya 所在城镇新建的现代铁路系统遇到了一个主要障碍：一条贯穿南北的高速公路。高速公路西侧已经建造并连接了 $\mathbf{W}$ 个车站，东侧则有 $\mathbf{E}$ 个车站。现在需要在西侧和东侧车站之间再建立一条连接，但由于高速公路的阻隔，这条连接必须通过一座立交桥来实现。 Ekiya 正在评估哪些车站组合最适合通过立交桥连接。作为评估的一部分，她想知道系统内路径的平均长度（以车站数量计）会如何随每种可能的连接方案而变化。 车站 $s$ 和 $t$ 之间的路径是指一个由不同车站组成的列表，该列表以 $s$ 开头、以 $t$ 结尾，且列表中任意两个连续车站之间存在连接。当前铁路系统中，西侧的 $\mathbf{W}$ 个车站通过 $\mathbf{W}-1$ 条连接构成，使得任意两个不同的西侧车站之间恰好存在一条路径。类似地，东侧的 $\mathbf{E}$ 个车站通过 $\mathbf{E}-1$ 条连接构成，使得任意两个不同的东侧车站之间也恰好存在一条路径。在建立连接一个西侧车站和一个东侧车站的立交桥后，任意两个不同车站之间将恰好存在一条路径。 一个完整地图是指具有 $\mathbf{W}+\mathbf{E}-1$ 条总连接，且任意两个车站之间恰好存在一条路径的地图。完整地图的平均距离是指所有不同车站对之间路径长度的平均值。路径长度是指定义该路径的车站列表长度减 1（例如，直接连接的两个车站之间的路径长度为 1）。 举例说明，下图展示了 $\mathbf{W}=2$ 个西侧车站和 $\mathbf{E}=3$ 个东侧车站的场景，图中显示了 2 种可能的立交桥方案。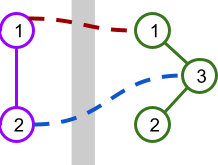  下表展示了每种立交桥方案下各车站对之间的路径长度。 | 起点 | 终点 | 1 ↔ 1 | 2 ↔ 3 | | :---: | :---: | :---: | :---: | | 西 1 | 西 2 | 1 | 1 | | 西 1 | 东 1 | 1 | 3 | | 西 1 | 东 2 | 3 | 3 | | 西 1 | 东 3 | 2 | 2 | | 西 2 | 东 1 | 2 | 2 | | 西 2 | 东 2 | 4 | 2 | | 西 2 | 东 3 | 3 | 1 | | 东 1 | 东 2 | 2 | 2 | | 东 1 | 东 3 | 1 | 1 | | 东 2 | 东 3 | 1 | 1 | | | 平均值： | 2 | 1.8 | 给定当前的车站和连接情况，以及立交桥连接方案的列表，请帮助 Ekiya 计算每种方案作为唯一立交桥连接时，所形成地图的平均距离。

输入的第一行给出测试用例的数量 $\mathbf{T}$。随后是 $\mathbf{T}$ 个测试用例。每个测试用例的第一行包含三个整数 $\mathbf{W}$、$\mathbf{E}$ 和 $\mathbf{C}$，分别表示西侧和东侧车站的数量，以及立交桥连接方案的数量。西侧车站编号为 $1$ 到 $\mathbf{W}$，东侧车站编号为 $1$ 到 $\mathbf{E}$。 测试用例的第二行包含 $\mathbf{W}-1$ 个整数 $\mathbf{X}_1, \mathbf{X}_2, \ldots, \mathbf{X}_{\mathbf{W}-1}$，表示西侧车站的第 $i$ 条现有连接连接了西侧车站 $i$ 和 $\mathbf{X}_i$。 测试用例的第三行包含 $\mathbf{E}-1$ 个整数 $\mathbf{F}_1, \mathbf{F}_2, \ldots, \mathbf{F}_{\mathbf{E}-1}$，表示东侧车站的第 $j$ 条现有连接连接了东侧车站 $j$ 和 $\mathbf{F}_j$。 最后，测试用例的最后 $\mathbf{C}$ 行描述了立交桥连接方案。其中第 $k$ 行包含两个整数 $\mathbf{A}_k$ 和 $\mathbf{B}_k$，表示第 $k$ 种立交桥方案将连接的西侧和东侧车站。

对于每个测试用例，输出一行 `Case #x:` $y_1$ $y_2$ $\cdots$ $y_{\mathbf{C}}$，其中 $x$ 是测试用例编号（从 $1$ 开始），$y_k$ 表示添加第 $k$ 种立交桥方案后所形成地图的平均距离。 $y_1$, $y_2$, $\ldots$, $y_k$ 只要与正确答案的绝对误差或相对误差不超过 $10^{-6}$ 即视为正确。有关误差说明及可接受的实数格式，请参阅 FAQ。

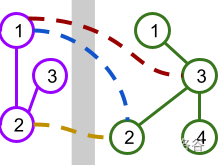
**样例解释** 样例 #1 已在题目描述中解释并图示。样例 #2 和样例 #3 图示如下。  **限制** - $1 \leq \mathbf{T} \leq 100$。 - $2 \leq \mathbf{W} \leq 10^{5}$。 - $2 \leq \mathbf{E} \leq 10^{5}$。 - 对所有 $i$，$i+1 \leq \mathbf{X}_{i} \leq \mathbf{W}$。（这意味着任意两个西侧车站之间恰好存在一条路径。） - 对所有 $j$，$j+1 \leq \mathbf{F}_{j} \leq \mathbf{E}$。（这意味着任意两个东侧车站之间恰好存在一条路径。） - 对所有 $k$，$1 \leq \mathbf{A}_{k} \leq \mathbf{W}$。 - 对所有 $k$，$1 \leq \mathbf{B}_{k} \leq \mathbf{E}$。 - 对所有 $k \neq \ell$，$(\mathbf{A}_{k}, \mathbf{B}_{k}) \neq (\mathbf{A}_{\ell}, \mathbf{B}_{\ell})$。（列出的每种立交桥连接方案均不相同。） **测试集 1（5 分，可见评测结果）** - 时间限制：20 秒。 - $1 \leq \mathbf{C} \leq 2$。 **测试集 2（7 分，隐藏评测结果）** - 时间限制：40 秒。 - $1 \leq \mathbf{C} \leq 10^{5}$。 翻译由 DeepSeek V3 完成