P12967 [CCO 2025] Tree Decorations

Mateo recently found the perfect decorations for his Christmas tree — more trees! Specifically, his Christmas tree is a rooted tree $T$ initially with $M$ nodes, all painted green. He has another rooted tree $D$ that he uses as a reference for his decorations. Mateo uses the following process to put on all of his decorations: - For each node $i$ in $D$, he creates a **copy** of the subtree rooted at $i$. Let this copy be $C_i$. Then, he paints the nodes of $C_i$ red. Finally, he chooses some green node in $T$ to be the parent of the root of $C_i$ by connecting them with an edge. After applying all the decorations, $T$ ends up containing $N$ nodes. Unfortunately, he realized that he had forgotten to record what $D$ is! To make things worse, he accidentally spilled water on $T$, washing off all the colour from the nodes. After all that, he labels the root of $T$ as 1, and then labels the rest of the nodes from 2 to $N$. The only information he currently has is the final state of $T$, as well as $M$. Help him find the number of possible $D$ that he could have started with, where two possibilities are considered different if they are structurally distinct. Rooted trees $A$ and $B$ are said to be structurally identical if and only if they have the same number of nodes $S$, and there is a way to label $A$'s nodes from 1 to $S$ and $B$'s nodes from 1 to $S$ such that: - Their roots are labeled the same. - Nodes labeled $x$ and $y$ in $A$ are connected by an edge if and only if nodes labeled $x$ and $y$ in $B$ are connected by an edge. Otherwise, $A$ and $B$ are considered structurally distinct.

The first line of input contains two space-separated integers $N$ and $M$. The next $N - 1$ lines each contain two space-separated integers $u_i$ and $v_i$ ($1 \leq u_i, v_i \leq N$, $u_i \neq v_i$), describing an edge in $T$ connecting nodes $u_i$ and $v_

Output the number of possible $D$ that he could have started with, where two possibilities are considered different if they are structurally distinct.

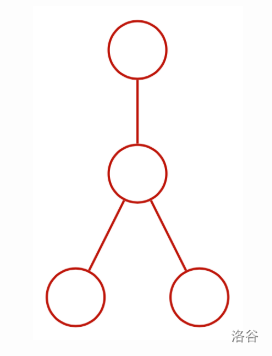
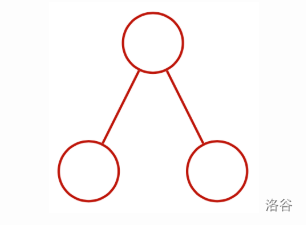
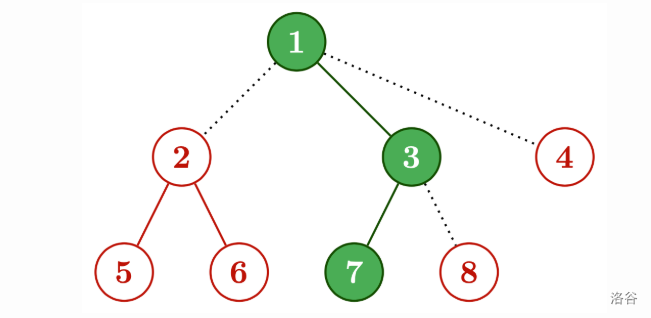
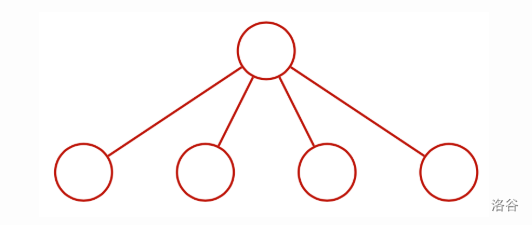
**Sample 1 Explanation** It is provable that the only possible $D$ is:  We can get $T$ the following way:  In the diagram above, the red parts are added as decorations, while the green, filled-in part represents the initial state of $T$. The dotted lines represent the edges connecting the decorations to the tree. 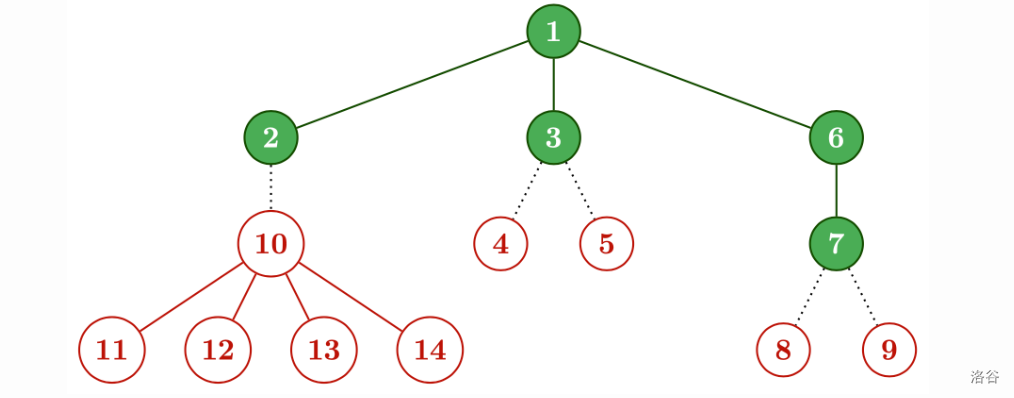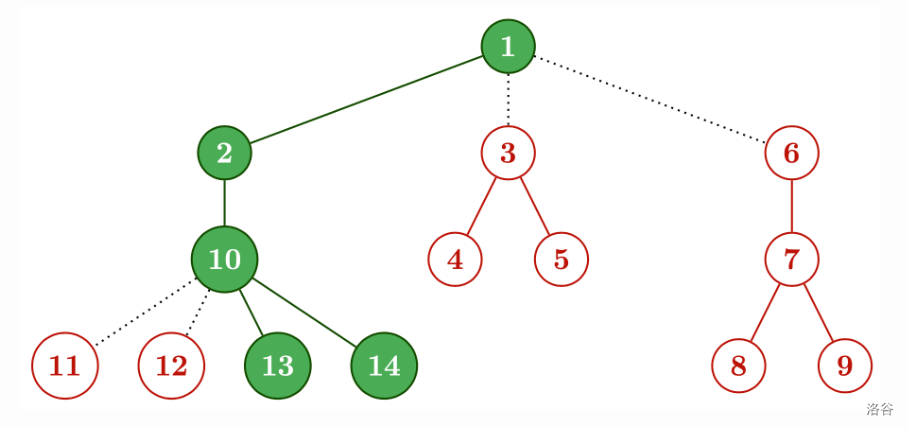**Sample 2 Explanation** The first possibility for $D$ is:  Using this, we can get $T$ the following way:  The second possibility for $D$ is:  Using this, we can get $T$ the following way:  The following table shows how the available $25$ marks are distributed: | Marks Awarded | Bounds on $N$ | Bounds on $M$ | |:---------------:|:---------------:|:----------------:| | 2 marks | $2 \leq N \leq 10$ | $M = 1$ | | 3 marks | $2 \leq N \leq 200$ | $M = 1$ | | 2 marks | $2 \leq N \leq 500000$ | $M = 1$ | | 6 marks | $2 \leq N \leq 200$ | $1 \leq M < N$ | | 4 marks | $2 \leq N \leq 2000$ | $1 \leq M < N$ | | 8 marks | $2 \leq N \leq 500000$ | $1 \leq M < N$ |