P12967 [CCO 2025] Tree Decorations
题目描述
**Mateo** 最近为他的圣诞树找到了完美的装饰品——更多的树!
具体来说,他的圣诞树是一棵初始有 $M$ 个节点、全部涂成绿色的有根树 $T$。他还有另一棵用作装饰参考的有根树 $D$。**Mateo** 通过以下步骤完成所有装饰:
- 对于 $D$ 中的每个节点 $i$,他创建一份以 $i$ 为根的子树**副本**,记为 $C_i$。然后,他将 $C_i$ 的所有节点涂成红色。最后,他选择 $T$ 中的某个绿色节点作为 $C_i$ 根节点的父节点,并通过一条边将它们连接起来。
完成所有装饰后,$T$ 最终包含 $N$ 个节点。不幸的是,他忘记记录 $D$ 的具体形态了!更糟的是,他不小心将水洒在 $T$ 上,导致所有节点的颜色都被洗掉了。之后,他将 $T$ 的根节点标记为 1,其余节点依次标记为 2 到 $N$。
目前他唯一掌握的信息是 $T$ 的最终形态以及 $M$ 的值。请帮助他计算可能的初始树 $D$ 的数量(若两棵树结构不同,则视为不同的可能性)。
若两棵有根树 $A$ 和 $B$ 满足以下条件,则称它们是**结构相同**的:
- 节点数 $S$ 相同;
- 存在一种对 $A$ 和 $B$ 的节点分别从 1 到 $S$ 的标号方式,使得:
- 它们的根节点标号相同;
- $A$ 中标号为 $x$ 和 $y$ 的节点之间有边当且仅当 $B$ 中标号为 $x$ 和 $y$ 的节点之间有边。
否则,$A$ 和 $B$ 被视为**结构不同**。
输入格式
第一行输入包含两个以空格分隔的整数 $N$ 和 $M$。
接下来的 $N - 1$ 行,每行包含两个以空格分隔的整数 $u_i$ 和 $v_i$($1 \leq u_i, v_i \leq N$,$u_i \neq v_i$),表示 $T$ 中连接节点 $u_i$ 和 $v_i$ 的一条边。
输出格式
输出可能的初始树 $D$ 的数量(结构不同的树视为不同情况)。
说明/提示
**样例 1 解释**
可以证明,唯一可能的 $D$ 如下图所示:
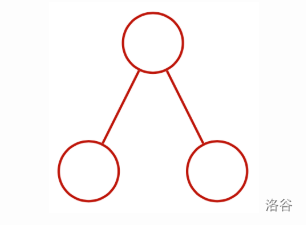
通过以下方式可以得到 $T$:
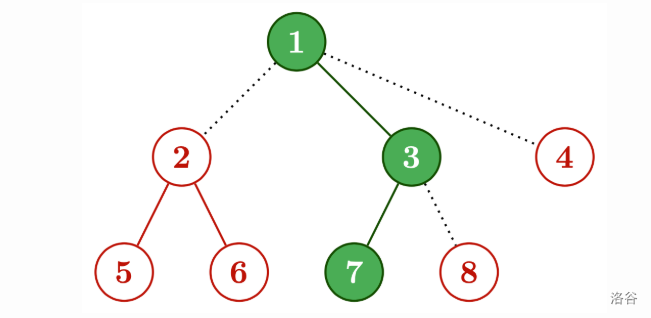
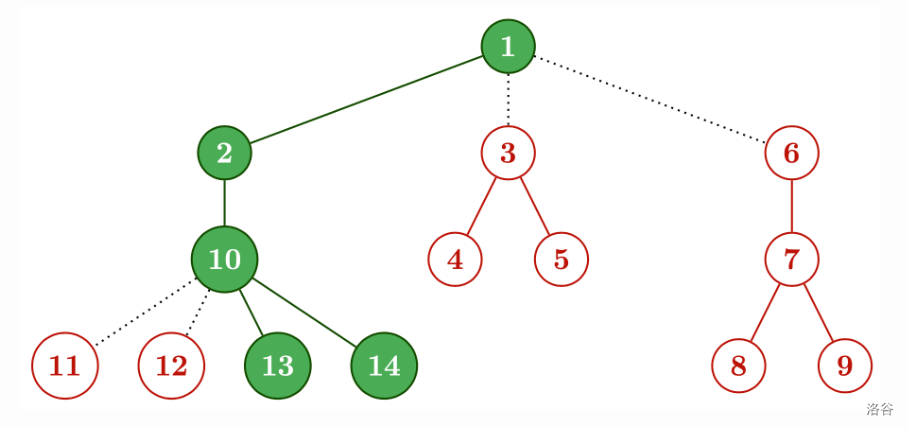
上图中,红色部分为添加的装饰,绿色填充部分表示 $T$ 的初始状态,虚线表示连接装饰品的边。
**样例 2 解释**
第一种可能的 $D$:
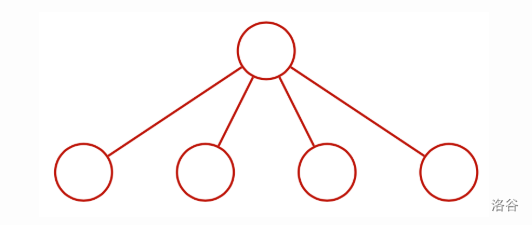
通过以下方式可以得到 $T$:
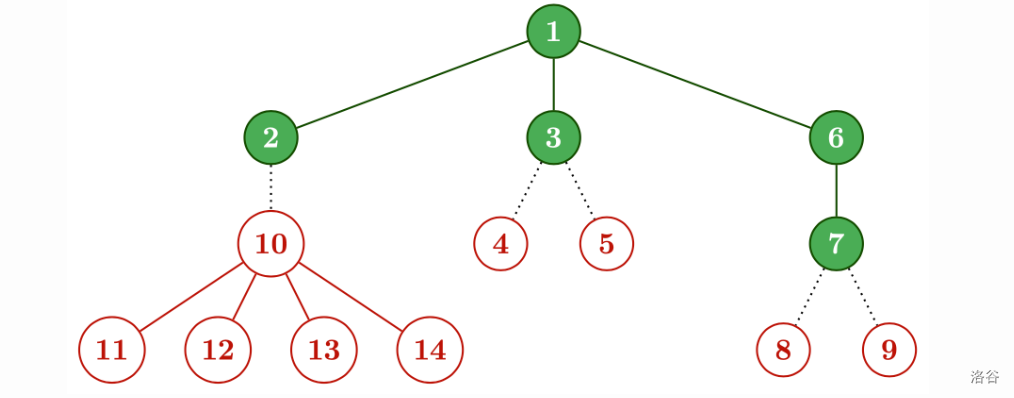
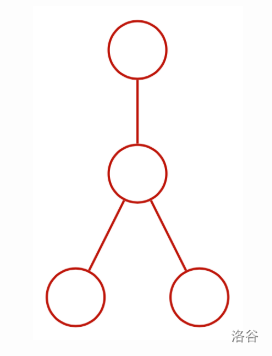
第二种可能的 $D$:
通过以下方式可以得到 $T$:
以下表格展示了 25 分的分布情况:
| 分值 | $N$ 的范围 | $M$ 的范围 |
|:------:|:-------------------:|:-------------------:|
| 2 分 | $2 \leq N \leq 10$ | $M = 1$ |
| 3 分 | $2 \leq N \leq 200$ | $M = 1$ |
| 2 分 | $2 \leq N \leq 500000$ | $M = 1$ |
| 6 分 | $2 \leq N \leq 200$ | $1 \leq M < N$ |
| 4 分 | $2 \leq N \leq 2000$ | $1 \leq M < N$ |
| 8 分 | $2 \leq N \leq 500000$ | $1 \leq M < N$ |
翻译由 DeepSeek V3 完成