P12991 [GCJ 2022 #1C] Squary

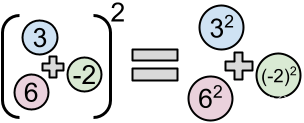
加法与平方运算不可交换。也就是说，一个整数列表中所有元素的和的平方，不一定等于这些元素各自的平方和。然而，某些列表满足这一性质，例如 $[3,-2,6]$，因为 $(3+(-2)+6)^{2}=49=3^{2}+(-2)^{2}+6^{2}$。我们将这样的列表称为**平方性列表**。  给定一个（不一定是平方性的）由较小整数构成的列表，我们想知道是否可以通过添加至少 $1$ 个、至多 $\mathbf{K}$ 个元素，使得最终的列表具有平方性。每个添加的元素必须是介于 $-10^{18}$ 和 $10^{18}$（含）之间的整数，且这些元素不必互不相同，也不必与初始列表中的元素不同。

输入的第一行给出测试用例的数量 $\mathbf{T}$。接下来是 $\mathbf{T}$ 个测试用例。每个测试用例由两行描述。第一行包含两个整数 $\mathbf{N}$ 和 $\mathbf{K}$，分别表示初始列表的元素数量和最多可添加的元素数量。第二行包含 $\mathbf{N}$ 个整数 $\mathbf{E}_{1}, \mathbf{E}_{2}, \ldots, \mathbf{E}_{\mathbf{N}}$，表示初始列表的 $\mathbf{N}$ 个元素。

对于每个测试用例，输出一行 `Case #x: y`，其中 $x$ 是测试用例编号（从 1 开始）。如果可以通过添加至少 1 个、至多 $\mathbf{K}$ 个元素（每个元素介于 $-10^{18}$ 和 $10^{18}$ 之间）使得列表元素的平方和等于元素和的平方，则 $y$ 应为 $z_{1} z_{2} \ldots z_{r}$，其中 $1 \leq r \leq \mathbf{K}$，$z_{i}$ 为添加的元素。如果无法实现，则 $y$ 应为 `IMPOSSIBLE`。

**样例解释** 在样例 #1 中，我们可以得到题目描述中的示例列表。 在样例 #2 中，必须恰好添加一个元素 $x$。此时整个列表的和为 $x$，其平方为 $x^{2}$。而所有元素的平方和为 $x^{2}+10^{2}+(-10)^{2}=x^{2}+200 \neq x^{2}$，因此该用例无法实现。 在样例 #3 中，$\left[-10^{18}, 10^{18}\right]$ 范围内的任意整数均为合法答案。 在样例 #4 中，注意输入可能包含重复元素，且通过添加元素创建更多重复也是合法的。 样例 2 符合测试集 2 的限制，但不会用于测试你的提交。 在附加样例的用例 #1 中，我们给出了题目描述中的示例列表（已是平方性列表），但需要至少添加一个元素。添加 0 可以保持列表的平方性。 在附加样例的用例 #3 中，我们展示了一种可能的合法答案。注意可以添加少于 $\mathbf{K}$ 个元素；此处 $\mathbf{K}=12$，但我们仅添加了 11 个元素。 **数据范围** - $1 \leq \mathbf{T} \leq 100$。 - $1 \leq \mathbf{N} \leq 1000$。 - 对所有 $i$，$-1000 \leq \mathbf{E}_{\mathbf{i}} \leq 1000$。 **测试集 1（9 分，可见判定）** - 时间限制：5 秒。 - $\mathbf{K}=1$。 **测试集 2（22 分，可见判定）** - 时间限制：10 秒。 - $2 \leq \mathbf{K} \leq 1000$。 翻译由 DeepSeek V3 完成