P12991 [GCJ 2022 #1C] Squary

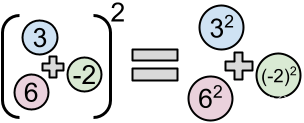
Addition and squaring do not commute. That is, the square of the sum of all elements of a list of integers is not necessarily equal to the sum of the squares of those same elements. However, this is true for some lists; one example is $[3,-2,6]$, because $(3+(-2)+6)^{2}=49=3^{2}+(-2)^{2}+6^{2}$. Let us call these lists squary.  Given a (not necessarily squary) list of relatively small integers, we want to know whether it is possible to add at least $1$ and at most $\mathbf{K}$ more elements such that the final list is squary. Each added element must be an integer between $-10^{18}$ and $10^{18}$, inclusive, and these do not have to be distinct from each other or from the initial list's elements.

The first line of the input gives the number of test cases, $\mathbf{T}$. $\mathbf{T}$ test cases follow. Each test case is described in two lines. The first line contains two integers $\mathbf{N}$ and $\mathbf{K}$, the number of elements of the initial list and the maximum number of elements you may add, respectively. The second line contains $\mathbf{N}$ integers $\mathbf{E}_{1}, \mathbf{E}_{2}, \ldots, \mathbf{E}_{\mathbf{N}}$, representing the $\mathbf{N}$ elements of the initial list.

For each test case, output one line containing `Case #x: y`, where $x$ is the test case number (starting from 1). If it is possible to add at least 1 and at most $\mathbf{K}$ elements (each an integer between $-10^{18}$ and $10^{18}$, inclusive) to the initial list such that the square of the sum of its elements equals the sum of the squares of its elements, $y$ should be $z_{1} z_{2} \ldots z_{r}$, where $1 \leq r \leq \mathbf{K}$ and the $z_{i}$ values are the additional elements. If there is no way to accomplish this, $y$ should be IMPOSSIBLE.

**Sample Explanation** In Sample Case #1, we can end up with the example list given in the problem statement. In Sample Case #2, we have to add exactly one element. If we call that element $x$, the sum of the entire list is $x$ and its square is $x^{2}$. The sum of the squares of all elements, on the other hand, is $x^{2}+10^{2}+(-10)^{2}=x^{2}+200 \neq x^{2}$, so the case is impossible. In Sample Case #3, any integer in the $\left[-10^{18}, 10^{18}\right]$ range is a valid answer. In Sample Case #4, notice that the input might contain duplicate elements, and that it is valid to create even more duplicates with the elements you choose to add. Sample 2 fits the limits of Test Set 2. It will not be run against your submitted solutions. In Case #1 of the additional samples, we are given the example list from the problem statement, which is already squary, but we need to add at least one element to it. Adding a 0 keeps the list squary. In Case #3 of the additional samples, we present one of multiple possible valid answers. Notice that it is permissible to add fewer than $\mathbf{K}$ elements; here $\mathbf{K}$ is 12 but we have only added 11 elements. **Limits** - $1 \leq \mathbf{T} \leq 100 .$ - $1 \leq \mathbf{N} \leq 1000 .$ - $-1000 \leq \mathbf{E}_{\mathbf{i}} \leq 1000$, for all $i$. **Test Set 1 (9 Pts, Visible Verdict)** - Time limit: 5 seconds. - $\mathbf{K}=1$. **Test Set 2 (22 Pts, Visible Verdict)** - Time limit: 10 seconds. - $2 \leq \mathbf{K} \leq 1000$.