P12992 [GCJ 2022 #1C] Intranets

Apricot Rules LLC 公司正在开发一种新的简化网络协议，并希望展示其路由算法。在他们的设计中，网络由编号从 1 到 $\mathbf{M}$ 的 $\mathbf{M}$ 台机器组成，每对机器之间通过一条直接链路连接。每条链路被赋予一个唯一的整数优先级，优先级值介于 1 到 $(\mathbf{M} \times (\mathbf{M} - 1)/2)$ 之间，每台机器根据这些优先级来路由流量。 遗憾的是，该路由算法过于激进，会将一台机器的所有流量都通过与其连接的最高优先级链路进行路由。这可能导致某些机器组与其他机器组隔离。 正式地说，我们说一台机器 $m$ 使用一条链路 $\ell$，当且仅当 $\ell$ 是与 $m$ 连接的优先级最高的链路。我们还称一条链路是**活跃的**，如果它被其连接的两台机器中的至少一台使用。根据链路优先级，原始网络将被划分为若干个不相交的**内联网**。两台机器属于同一个内联网，当且仅当它们之间存在一条仅由活跃链路组成的路径。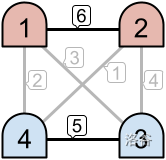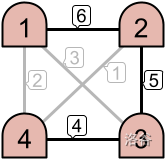   例如，如上图左侧所示，只有优先级为 6 和 5 的链路是活跃的。这形成了两个不相交的内联网。然而，右侧的示例中有三条活跃链路，结果形成了一个包含所有 4 台机器的内联网。 作为 Apricot Rules LLC 公司质量保证团队的一员，你正在调查这个问题的严重程度。你感兴趣的是，如果优先级是从 $(\mathbf{M} \times (\mathbf{M} - 1)/2)!$ 种可能的分配方式中均匀随机选择的，那么恰好形成 $\mathbf{K}$ 个内联网的概率是多少。

输入的第一行给出测试用例的数量 $\mathbf{T}$。随后是 $\mathbf{T}$ 个测试用例。每个测试用例由一行描述，包含两个整数 $\mathbf{M}$ 和 $\mathbf{K}$，分别表示机器的数量和目标内联网的数量。

对于每个测试用例，输出一行 `Case #x: y`，其中 $x$ 是测试用例编号（从 1 开始），$y$ 是所求概率对质数 $10^{9}+7$（$1000000007$）取模后的结果。具体定义如下：将概率表示为不可约分数 $p/q$（其中 $p$ 和 $q$ 是非负整数，且 $p+q$ 最小），则 $y$ 必须等于 $p \cdot q^{-1} \bmod 10^{9}+7$，其中 $q^{-1}$ 是 $q$ 在模 $10^{9}+7$ 下的模逆元。可以证明，在本问题的约束条件下，这样的 $y$ 总是存在且唯一。

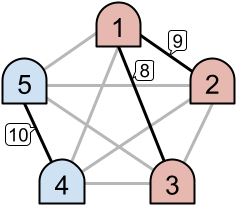
**样例解释** 在样例 #1 中，考虑以下情况。设 $\mathbf{M}=5$ 台机器为 $1,2,3,4,5$，并将连接机器 $a$ 和机器 $b$ 的链路记为 $(a, b)$。假设链路 $(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)$ 的优先级分别为 $9,8,7,6,5,4,3,2,1,10$。那么机器 1 和 2 使用链路 $(1,2)$，机器 3 使用链路 $(1,3)$，机器 4 和 5 使用链路 $(4,5)$。因此，三条链路 $(1,2),(1,3),(4,5)$ 是活跃的，形成了两个内联网 $\{1,2,3\}$ 和 $\{4,5\}$。由于 $\mathbf{K}=2$，这种情况计入答案。  我们可以发现，在 $10! = 3628800$ 种优先级分配方式中，有 $1555200$ 种方式会恰好形成 $2$ 个内联网，因此概率为 $3/7$。 在样例 #2 中，概率为 $4/7$。 在样例 #3 中，概率为 $1/21$。 **数据范围** - $1 \leq \mathbf{T} \leq 50$。 - $1 \leq \mathbf{K} \leq \mathbf{M}/2$。 **测试集 1（17 分，可见判定）** - 时间限制：20 秒。 - $2 \leq \mathbf{M} \leq 50$。 **测试集 2（27 分，隐藏判定）** - 时间限制：60 秒。 - $2 \leq \mathbf{M} \leq 5 \times 10^{5}$。 翻译由 DeepSeek V3 完成