P12993 [GCJ 2022 #2] Spiraling Into Control

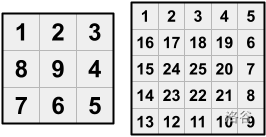
As punishment for being naughty, Dante has been trapped in a strange house with many rooms. The house is an $\mathbf{N} \times \mathbf{N}$ grid of rooms, with $\mathbf{N}$ odd and greater than 1. The upper left room is numbered 1 , and then the other rooms are numbered $2,3, \ldots, \mathbf{N}^{2}$, in a clockwise spiral pattern. That is, the numbering proceeds along the top row of the grid and then makes a 90 degree turn to the right whenever a grid boundary or an already numbered room is encountered, and finishes in the central room of the grid. Because $\mathbf{N}$ is odd, there is always a room in the exact center of the house, and it is always numbered $\mathbf{N}^{2}$. For example, here are the room numberings for houses with $\mathbf{N}=3$ and $\mathbf{N}=5$:  Dante starts off in room 1 and is trying to reach the central room (room $\mathbf{N}^{2}$ ). Throughout his journey, he can only make moves from his current room to higher-numbered, adjacent rooms. (Two rooms must share an edge - not just a corner - to be adjacent.) Dante knows that he could walk from room to room in consecutive numerical order - i.e., if he is currently in room $x$, he would move to room $x+1$, and so on. This would take him exactly $\mathbf{N}^{2}-1$ moves. But Dante wants to do things his way! Specifically, he wants to reach the central room in exactly $\mathbf{K}$ moves, for some $\mathbf{K}$ strictly less than $\mathbf{N}^{2}-1$. Dante can accomplish this by taking one or more shortcuts. A shortcut is a move between rooms that are not consecutively numbered. 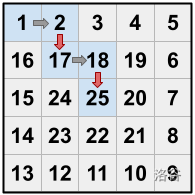For example, in the $5 \times 5$ house above, - If Dante is at $1$, he cannot move to $17$, but he can move to $2$ or to $16$. The move to $2$ is not a shortcut, since $1+1=2$. The move to $16$ is a shortcut, since $1+1 \neq 16$. - From $2$, it is possible to move to $3$ (not a shortcut) or to $17$ (a shortcut), but not to $1,16$, or $18$. - From $24$, Dante can only move to $25$ (not a shortcut). - It is not possible to move out of room $25$. As a specific example using the $5 \times 5$ house above, suppose that $\mathbf{K}=4$. One option is for Dante to move from $1$ to $2$, then move from $2$ to $17$ (which is a shortcut), then move from $17$ to $18$, then move from $18$ to $25$ (which is another shortcut). This is illustrated below (the red arrows represent shortcuts):  Can you help Dante find a sequence of exactly $\mathbf{K}$ moves that gets him to the central room, or tell him that it is impossible?

The first line of the input gives the number of test cases, $\mathbf{T}$. $\mathbf{T}$ test cases follow. Each test case consists of one line with two integers $\mathbf{N}$ and $\mathbf{K}$, where $\mathbf{N}$ is the dimension of the house (i.e. the number of rows of rooms, which is the same as the number of columns of rooms), and $\mathbf{K}$ is the exact number of moves that Dante wants to make while traveling from room 1 to room $\mathbf{N}^{2}$.

For each test case, output one line containing `Case x: y`, where $x$ is the test case number (starting from 1). If no valid sequence of exactly $\mathbf{K}$ moves will get Dante to the central room, $y$ must be IMPOSSIBLE. Otherwise, $y$ must be an integer: the number of times that Dante takes a shortcut, as described above. (Notice that because Dante wants to finish in strictly less than $\mathbf{N}^{2}-1$ moves, he must always use at least one shortcut.) Then, output $y$ more lines of two integers each. The $i$-th of these lines represents the $i$-th time in Dante's journey that he takes a shortcut, i.e., he moves from some room $a_{i}$ to another room $b_{i}$ such that $a_{i}+1

**Sample Explanation** Sample Case #1 is described in the problem statement. Dante's route is $1 \rightarrow 2 \rightarrow 17 \rightarrow 18 \rightarrow 25$. Because $1 \rightarrow 2$ and $17 \rightarrow 18$ are moves between consecutively numbered rooms, they are not included in the output. Only the shortcuts $(2 \rightarrow 17$ and $18 \rightarrow 25)$ are included. In Sample Case #2, there is no solution. (Recall that there is no way for Dante to move diagonally.) In Sample Case #3, observe that $22$ appears both as the end of one shortcut and the start of the next. It would not be valid to include the line $11\ 22\ 25$ in the output; each line must represent a single shortcut.  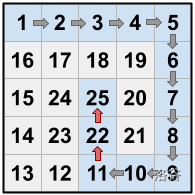There is another solution that uses only one shortcut: Dante can move from $1 \rightarrow 2 \rightarrow 3 \rightarrow 4 \rightarrow 5 \rightarrow 6$, then move from $6 \rightarrow 19$ (a shortcut), then move from $19 \rightarrow 20 \rightarrow 21 \rightarrow 22 \rightarrow 23 \rightarrow 24 \rightarrow 25$. This is also valid; there is no requirement to minimize (or maximize) the number of shortcuts taken. In Sample Case #4, Dante cannot get to the central room ($9$, in this case) in just one move. **Limits** - $1 \leq \mathbf{T} \leq 100$. - $1 \leq \mathbf{K}