P12995 [GCJ 2022 #2] Saving the Jelly

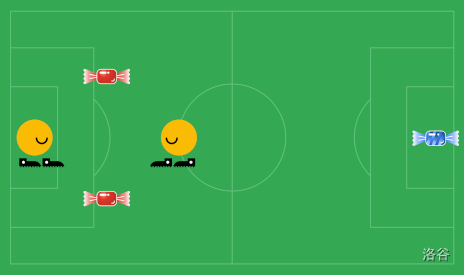
Jolly 先生正在教编号为 1 到 $\mathbf{N}$ 的 $\mathbf{N}$ 个孩子踢足球（或称 soccer，针对美国读者）。他习惯在比赛场地上放置糖果，每个孩子一颗。比赛结束后，每个孩子可以拿走并吃掉一颗作为奖励。 孩子们在比赛后很累，所以每个孩子都想拿离自己最近的糖果（使用欧几里得距离计算）。这可能导致冲突——如果同一颗糖果是多个孩子最近的。为避免这种情况，比赛结束后所有孩子停在原地，Jolly 先生会依次点名。当被点到名时，孩子会拿走离自己最近的糖果（当然，只能选未被拿走的糖果）。当有多颗糖果距离最近且相同时，Jolly 先生可以决定孩子拿哪一颗。  这个方法一直很有效，但今天出问题了！Jolly 先生在布置糖果时，不小心把他准备在孩子们回家后享用的蓝莓果冻也放在了场地上。现在场上有 $\mathbf{N}$ 个孩子和 $\mathbf{N}+1$ 颗糖果。糖果编号为 1 到 $\mathbf{N}+1$，其中 1 号是 Jolly 先生的蓝莓果冻。是否存在一种点名顺序，使得最后剩下的糖果正好是蓝莓果冻？

第一行输入测试用例数量 $\mathbf{T}$。随后 $\mathbf{T}$ 个测试用例，每个用例第一行是一个整数 $\mathbf{N}$ 表示孩子数量。接下来 $\mathbf{N}$ 行描述孩子的位置，每行两个整数 $\mathbf{X}_{\mathbf{i}}$ 和 $\mathbf{Y}_{\mathbf{i}}$ 表示第 $i$ 个孩子的坐标。随后 $\mathbf{N}+1$ 行描述糖果位置，其中第一颗是蓝莓果冻，每行两个整数 $\mathbf{X}_{\mathbf{j}}$ 和 $\mathbf{Y}_{\mathbf{j}}$ 表示第 $j$ 颗糖果的坐标。

对于每个测试用例，输出一行 `Case #x: y`，其中 $x$ 是用例编号（从 1 开始）。若无法保留蓝莓果冻，$y$ 为 IMPOSSIBLE；否则为 POSSIBLE。若可能，还需输出 $\mathbf{N}$ 行表示点名顺序和选择的糖果，每行两个整数 $A_{i}$ 和 $B_{i}$，表示孩子 $A_{i}$ 被点名并选择糖果 $B_{i}$（选择时 $B_{i}$ 必须是该孩子最近的糖果之一）。

**样例解释** 样例 #1 如上图所示。每个孩子到两颗非果冻糖果的距离相等。解决方案中，Jolly 先生让 2 号孩子拿 2 号糖果，1 号孩子拿 3 号糖果，成功保留 1 号糖果（蓝莓果冻）。 样例 #2 中，唯一的孩子离蓝莓果冻比其他糖果更近，Jolly 先生无法保住果冻。 样例 #3 展示了一种可能的解，实际上可以任意顺序点名。 样例 #4 中注意孩子可能位置重合、糖果可能位置重合、孩子和糖果也可能位置重合。 **数据范围** - $1 \leq \mathbf{T} \leq 100$ - 所有坐标的绝对值不超过 $10^{9}$ **测试集 1（10 分，可见判定）** - 时间限制：10 秒 - $1 \leq \mathbf{N} \leq 10$ **测试集 2（18 分，隐藏判定）** - 时间限制：45 秒 - $1 \leq \mathbf{N} \leq 1000$ 翻译由 DeepSeek V3 完成