P1299 Hole Cutting Machine
Description
Assistants at the headquarters often need to cut holes of various shapes in a large sheet of paper. They have just purchased a new hole cutting machine, which is much more convenient and flexible than the one they used before. They want to write a program to determine what happens after a sequence of complex cuts; in particular, they want to know how many holes are formed in the paper.
The figure below shows several patterns formed after cutting.
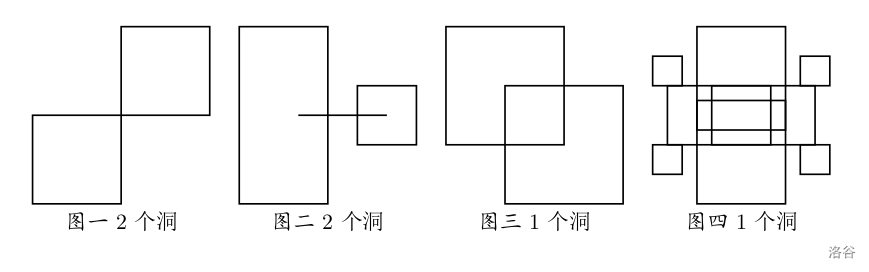
Input Format
The first line contains an integer $N$, the number of cutting operations, with $1 \le N \le 100$. Each of the next $N$ lines gives one precise cut, described by four space-separated integers $x_1, y_1, x_2, y_2$, with $-1000 \le x_1, y_1, x_2, y_2 \le 1000$. Here, $x_1$ and $y_1$ are the coordinates where the cut starts, and $x_2$ and $y_2$ are the coordinates where the cut ends. You may assume all cutting points lie on the paper and never go out of bounds. Each cut is an axis-aligned segment (parallel to the $x$ or $y$ axis).
Output Format
Output a single integer on one line, the number of separate holes on the paper after all cuts are completed. Note that the area of any hole is at least $1$ square unit.
Explanation/Hint
Translated by ChatGPT 5