P13001 [GCJ 2022 Finals] Wonderland Chase

**Alice** 被困在仙境的迷宫中，正被**红心皇后**和她的传令官追赶！迷宫由 $\mathbf{J}$ 个编号为 1 到 $\mathbf{J}$ 的交叉点和 $\mathbf{C}$ 条双向走廊连接而成。 **Alice** 和**红心皇后**轮流移动，双方始终知道对方的位置。每次移动（无论是谁）可以选择停留在当前交叉点，或通过走廊移动到相邻的交叉点。 然而，皇后的传令官会提前宣布皇后下一步的移动计划。这意味着在任何人移动之前，他会先宣布皇后的第一步移动。接着，**Alice** 先移动。之后，每次皇后移动时，她必须遵守之前的宣布，并决定下一步移动以便传令官宣布。**Alice** 会听到这些宣布，因此她总是能在自己移动前知道皇后的下一步计划。  如果 **Alice** 和皇后在任意一方移动后处于同一交叉点，则 **Alice** 被抓住。否则，追逐继续。若在总共 $10^{9}$ 次移动（**Alice** 和皇后各占一半）后，两人仍未处于同一交叉点，则皇后会放弃，**Alice** 安全逃脱。 **Alice** 会以最优策略选择移动以逃脱。若无法逃脱，她会选择最大化被抓住前的移动次数。皇后则会以最优策略尝试在尽可能少的移动次数内抓住 **Alice**。 给定迷宫的布局以及 **Alice** 和皇后的初始位置，判断 **Alice** 是否会被皇后抓住，如果是，计算需要多少次移动。

输入的第一行包含测试用例的数量 $\mathbf{T}$。随后是 $\mathbf{T}$ 个测试用例。每个测试用例的第一行包含四个整数 $\mathbf{J}$、$\mathbf{C}$、$\mathbf{A}$ 和 $\mathbf{Q}$：分别表示交叉点数量、走廊数量、**Alice** 的起始交叉点和皇后的起始交叉点。接着是 $\mathbf{C}$ 行，每行包含两个整数 $\mathbf{U}_i$ 和 $\mathbf{V}_i$，表示第 $i$ 条走廊双向连接交叉点 $\mathbf{U}_i$ 和 $\mathbf{V}_i$。

对于每个测试用例，输出一行 `Case #x: y`，其中 $x$ 是测试用例编号（从 1 开始），$y$ 为 `SAFE` 表示 **Alice** 能在 $10^9$ 次移动内避免被抓住；否则 $y$ 是皇后抓住 **Alice** 所需的总移动次数（包括 **Alice** 和皇后的移动）。

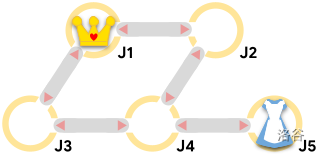
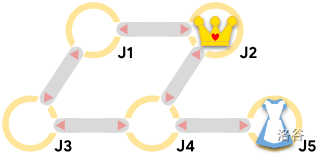
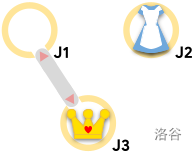
样例 #1 对应题目描述中的图示。**Alice** 的最优第一步是移动到交叉点 4。 样例 #2 与样例 #1 相同，但皇后起始于交叉点 2。皇后可以通过先宣布移动到交叉点 4 来抓住 **Alice**。若 **Alice** 移动到交叉点 4，她将在 2 次移动后被抓住。 **Alice** 可以选择停留，直到皇后移动到交叉点 5，从而将捕获时间延长至 4 次移动。  样例 #3 中，皇后无论如何都无法到达 **Alice** 所在位置。  样例 #4 中，皇后可以宣布直接移动到 **Alice** 当前所在的交叉点。**Alice** 必须在皇后移动前行动。若 **Alice** 移动到皇后所在位置，她会立即被抓住；若停留原地，则会在皇后移动时被抓住。第二种选择更优，因为需要 2 次总移动（**Alice** 和皇后各一次）而非 1 次。  **限制条件** - $1 \leq \mathbf{T} \leq 100$。 - $1 \leq \mathbf{A} \leq \mathbf{J}$。 - $1 \leq \mathbf{Q} \leq \mathbf{J}$。 - $\mathbf{A} \neq \mathbf{Q}$。 - 对所有 $i$，$1 \leq \mathbf{U}_i < \mathbf{V}_i \leq \mathbf{J}$。 - 对所有 $i \neq j$，$(\mathbf{U}_i, \mathbf{V}_i) \neq (\mathbf{U}_j, \mathbf{V}_j)$。 **测试集 1（可见判定）** - 时间限制：10 秒。 - $2 \leq \mathbf{J} \leq 30$。 - $1 \leq \mathbf{C} \leq 60$。 **测试集 2（隐藏判定）** - 时间限制：60 秒。 - $2 \leq \mathbf{J} \leq 10^5$。 - $1 \leq \mathbf{C} \leq 2 \times 10^5$。 翻译由 DeepSeek V3 完成