P13004 [GCJ 2022 Finals] Schrödinger and Pavlov

_本题目中所有故事、名称、角色和情节均为虚构。如有雷同，纯属巧合。_ 1935 年，两位诺贝尔奖得主的会面产生了惊人的结果。著名物理学家**薛定谔**邀请著名生理学家**巴甫洛夫**参观他的"猫在箱子里"的实验。巴甫洛夫带着他的狗一同前来以继续自己的研究，两者的实验相结合产生了有趣的现象。 薛定谔有一排 $\mathbf{N}$ 个箱子。某些箱子中肯定有一只猫，某些箱子肯定没有猫，还有些箱子可能有也可能没有猫。每个箱子只能容纳一只猫。每个箱子还配备了一个特殊的**量子隧道**，允许箱子里的猫移动到另一个特定的箱子（前提是目标箱子是空的）。隧道的运作是单向的。 猫通常很安静，除非受到惊吓才会使用隧道。当一位不速之客按响门铃时，巴甫洛夫的狗立即兴奋起来，开始边跑边叫。狗从 1 号箱子开始，一直跑到 $\mathbf{N}$ 号箱子。当它经过一个有猫的箱子时，会惊吓到里面的猫。受惊的猫会检查可用的隧道：如果目标箱子是空的，就会通过隧道逃跑；如果目标箱子已被占据，猫就会留在原地。同一只猫可能会被多次惊吓（如果它移动到了狗还未经过的箱子），每次受惊时都会以相同的方式检查隧道（但每次只能使用新位置的隧道）。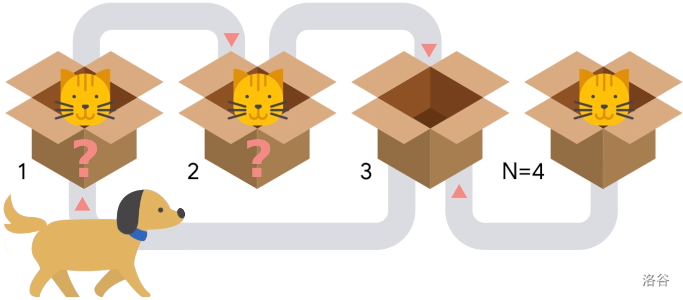  当狗最终停在最后一个箱子旁时，巴甫洛夫问薛定谔最后一个箱子里是否有猫。薛定谔（不出所料）回答说他不知道。巴甫洛夫意识到，答案取决于那些未知箱子中是否有猫。由于有 $k$ 个未知箱子，共有 $2^k$ 种可能的**初始配置**（每种对应未知箱子状态的一种组合）。巴甫洛夫建议他们应该计算有多少种初始配置会导致最后一个箱子里有猫。你需要重现这个计算过程。由于结果可能非常大，只需输出其对质数 $10^9 + 7$（1000000007）取模的值。 *在本题描述过程中，没有猫、狗或诺贝尔奖得主受到伤害。*

输入的第一行给出测试用例数量 $\mathbf{T}$。随后每个测试用例由三行组成：第一行是整数 $\mathbf{N}$（箱子数量，编号为 1 到 $\mathbf{N}$）；第二行是长度为 $\mathbf{N}$ 的字符串 $\mathbf{S}$，其中第 $i$ 个字符表示 $i$ 号箱子的初始状态（'c'表示有猫，'.'表示无猫，'?'表示未知）；第三行包含 $\mathbf{N}$ 个整数 $\mathbf{B}_1, \mathbf{B}_2, \dots, \mathbf{B}_\mathbf{N}$，表示从 $i$ 号箱子出发的隧道通向 $\mathbf{B}_i$ 号箱子。

对于每个测试用例，输出一行 `Case #x: y`，其中 $x$ 是测试用例编号（从 1 开始），$y$ 是会导致最后一个箱子最终有猫的初始配置数量（模 $10^9 + 7$）。

**样例解释** 样例 #1 的情况如题目描述所示。4 种可能的初始配置中，只有 `CC.C` 会导致最后一个箱子最终有猫。 样例 #2 中，由于没有隧道通向最后一个箱子，只有当最后一个箱子初始有猫时才可能最终有猫。经分析共有 2 种符合条件的配置。 样例 #3 中，要使最后一个箱子最终有猫，必须满足：5 号箱子初始有猫，且至少还有一个其他箱子有猫。符合条件的配置共有 $2^4 - 1 = 15$ 种。 样例 #4 中，对于所有 $2^k$ 种可能的初始配置，最后一个箱子最终都会有猫。 **限制条件** - $1 \leq \mathbf{T} \leq 1234$ - $\mathbf{S}$ 的长度等于 $\mathbf{N}$ - $\mathbf{S}$ 的每个字符是大写的 'c'、'.' 或 '?' - $1 \leq \mathbf{B}_i \leq \mathbf{N}$ 且 $\mathbf{B}_i \neq i$（所有 $i$） **测试集 1（8 分，可见判定）** - $1 \leq \mathbf{N} \leq 100$ - $i - 5 \leq \mathbf{B}_i \leq i + 5$（所有隧道都连接到附近的箱子） **测试集 2（42 分，隐藏判定）** - $1 \leq \mathbf{N} \leq 5000$ 翻译由 DeepSeek V3 完成