P13005 [GCJ 2022 Finals] Triangles
题目描述
给定二维平面上的一个点集 $P$,包含 $\mathbf{N}$ 个互不相同的点。你需要找到一个最大的三角形集合满足以下条件:
* 集合中每个三角形的顶点都来自 $P$,且 $P$ 中的每个点最多作为一个三角形的一个顶点。
* 集合中的每个三角形面积必须为正(即三个顶点不共线)。
* 对于集合中任意两个三角形的边,它们的交集要么为空,要么是其中一条边的端点。
* 对于集合中任意两个三角形,它们内部区域的交集要么为空,要么完全等于其中一个三角形。
下图展示的三角形集合满足以上所有条件:
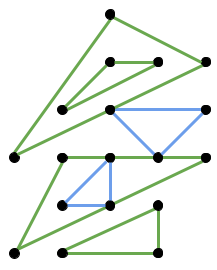
而下图中任意一对黄色和红色三角形的组合都不满足条件:
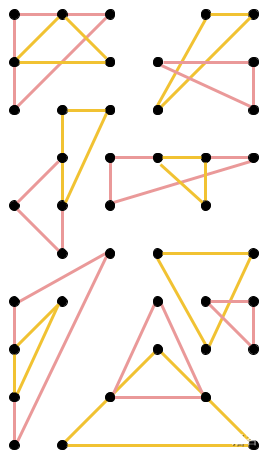
输入格式
输入的第一行给出测试用例的数量 $\mathbf{T}$。随后每个测试用例的第一行是一个整数 $\mathbf{N}$,接着 $\mathbf{N}$ 行,每行包含两个整数 $\mathbf{X}_i$ 和 $\mathbf{Y}_i$,表示第 $i$ 个点的坐标。
输出格式
对于每个测试用例,首先输出一行 `Case #x: y`,其中 $x$ 是测试用例编号(从 1 开始),$y$ 是满足条件的三角形集合的最大大小。然后输出 $y$ 行,每行三个整数 $p_j\ q_j\ r_j$,表示第 $j$ 个三角形由输入中的第 $p_j$、$q_j$ 和 $r_j$ 个点组成(点从 1 开始编号)。
说明/提示
**样例解释**
样例 #1 如下图所示。注意存在其他有效的构造方式也能达到最大三角形数量:

样例 #2 如下图所示。同样存在其他有效的构造方式能组成 2 个三角形:
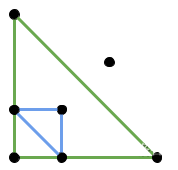
样例 #3 中,所有给定点共线,因此无法组成有效的三角形。
**限制条件**
- $1 \leq \mathbf{T} \leq 100$
- $-10^9 \leq \mathbf{X}_i \leq 10^9$(所有 $i$)
- $-10^9 \leq \mathbf{Y}_i \leq 10^9$(所有 $i$)
- 所有点的坐标互不相同
**测试集 1(8 分,可见判定)**
- $3 \leq \mathbf{N} \leq 12$
**测试集 2(42 分,隐藏判定)**
- $3 \leq \mathbf{N} \leq 3000$
翻译由 DeepSeek V3 完成