P13011 【MX-X13-T6】「KDOI-12」能做到的也只不过是静等缘分耗尽的那一天。
题目背景
待到缘分耗尽,关系断裂,我们还会在一起吗?
题目描述
对于一个排列 $p_{1\sim n}$,建出其大根[笛卡尔树](https://www.luogu.com.cn/problem/P5854),并断开每个点与其右儿子(如果存在)的连边,记最后所成的森林为 $T(p)$。
例如 $p_{1\sim 5} = [1, 3, 2, 5, 4]$,其大根笛卡尔树与 $T(p)$ 分别如下图:
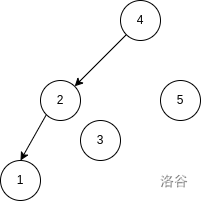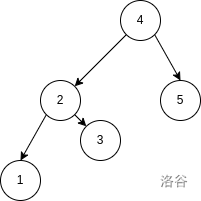
在给定 $n, x, y$ 的情况下,你需要回答,在 $n!$ 种 $1\sim n$ 的排列 $p_{1\sim n}$ 中,有多少种 $p$ 使得节点 $x$ 与节点 $y$ 在 $T(p)$ 中属于同一棵树。**节点指的是编号而非在 $p$ 中的权值。**
由于答案可能很大,输出的答案需要对一个质数 $P$ 取模。
输入格式
**本题有多组测试数据。**
第一行,两个正整数 $T, P$,表示测试数据组数与模数。**保证 $\bm P$ 为质数**。对于每组测试数据:
* 仅一行,三个正整数 $n, x, y$。
输出格式
对于每组测试数据,一行,一个非负整数,表示满足题目条件的排列数量,对 $P$ 取模。
说明/提示
**【样例解释】**
对于样例的第一组测试数据:有 $[1, 2, 3, 4], [1, 3, 2, 4], [2, 1, 3, 4], [2, 3, 1, 4], [3, 1, 2, 4], [3, 2, 1, 4]$ 共 $6$ 种排列满足条件。
对于样例的第二组测试数据:任意 $1\sim 4$ 的排列均满足条件。
**【数据范围】**
**本题使用捆绑测试。**
| 子任务编号 | 分值 | $n\leq$ | $T\leq$ | 特殊性质 |
|:--:|:--:|:--:|:--:|:--:|
| $1$ | $5$ | $8$ | $10^6$ | 无 |
| $2$ | $15$ | $2000$ | $2000$ | 无 |
| $3$ | $15$ | $2000$ | $10^6$ | 无 |
| $4$ | $25$ | $5\times10^6$ | $20$ | 无 |
| $5$ | $15$ | $10^5$ | $10^6$ | A |
| $6$ | $25$ | $5\times10^6$ | $10^6$ | 无 |
* 特殊性质 A:$P=998244353$。
对于所有数据:$1\leq T\leq10^6$,$1\le x, y\le n\le 5\times 10^6$,$10^8\le P\le 10^9 + 7$ 且 $P$ 为质数。
**【提示】**
请使用较快的读入方式。