P13011 【MX-X13-T6】"All I Can Do Is Quietly Wait for the Day When Fate Runs Out"

When fate runs out and relationships break, will we still be together?

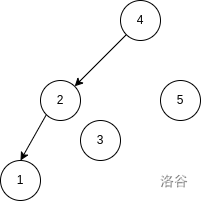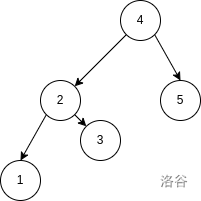
For a permutation $p_{1\sim n}$, construct its **max-heap Cartesian tree**, then disconnect the edge between each node and its right child (if it exists). Denote the resulting forest as $T(p)$. For example, consider $p_{1\sim 5} = [1, 3, 2, 5, 4]$. The max-heap Cartesian tree and $T(p)$ are shown below:  Given $n, x, y$, you need to determine how many of the $n!$ permutations of $1\sim n$ satisfy that nodes $x$ and $y$ belong to the same tree in $T(p)$. **Nodes are identified by their indices, not their values in $p$.** Since the answer may be large, output it modulo a prime $P$.

**This problem contains multiple test cases.** The first line contains two positive integers $T$ and $P$, representing the number of test cases and the modulo. **It is guaranteed that $\bm{P}$ is a prime.** For each test case: - One line with three positive integers $n, x, y$.

For each test case, output a non-negative integer indicating the number of valid permutations modulo $P$.

### Sample Explanation For the first test case, the following $6$ permutations satisfy the condition: $[1, 2, 3, 4], [1, 3, 2, 4], [2, 1, 3, 4], [2, 3, 1, 4], [3, 1, 2, 4], [3, 2, 1, 4]$. For the second test case, all $1\sim 4$ permutations are valid. ### Constraints **This problem uses bundling tests.** | Subtask | Points | $n\leq$ | $T\leq$ | Special Constraints | |:------:|:------:|:------:|:------:|:------------------:| | $1$ | $5$ | $8$ | $10^6$ | None | | $2$ | $15$ | $2000$ | $2000$ | None | | $3$ | $15$ | $2000$ | $10^6$ | None | | $4$ | $25$ | $5\times10^6$ | $20$ | None | | $5$ | $15$ | $10^5$ | $10^6$ | A | | $6$ | $25$ | $5\times10^6$ | $10^6$ | None | - Special Constraint A: $P=998244353$. For all test cases: - $1 \leq T \leq 10^6$, - $1 \le x, y \le n \le 5 \times 10^6$, - $10^8 \le P \le 10^9 + 7$ and $P$ is a prime. ### Hint Please use a fast input method. --- *Translation by DeepSeek V3.*