P1301 Devil City

In a rectangular “Devil City” divided into $N \times M$ square rooms, an explorer must follow the rules below to move by jumping. He must enter at $(1, 1)$ and exit at $(N, M)$. On the wall of every room there is a magic number, which is a natural number from $1$ to $13$ inclusive. The explorer can imagine any of the $8$ directions (horizontal, vertical, or diagonal), and then make a spatial jump passing through $X$ consecutive rooms in that direction, where $X$ is the magic number of the room he is currently in. However, if the number of rooms available in that direction is less than $X$, he does not jump and must imagine another direction. In addition, the explorer cannot make two consecutive jumps in the same direction.  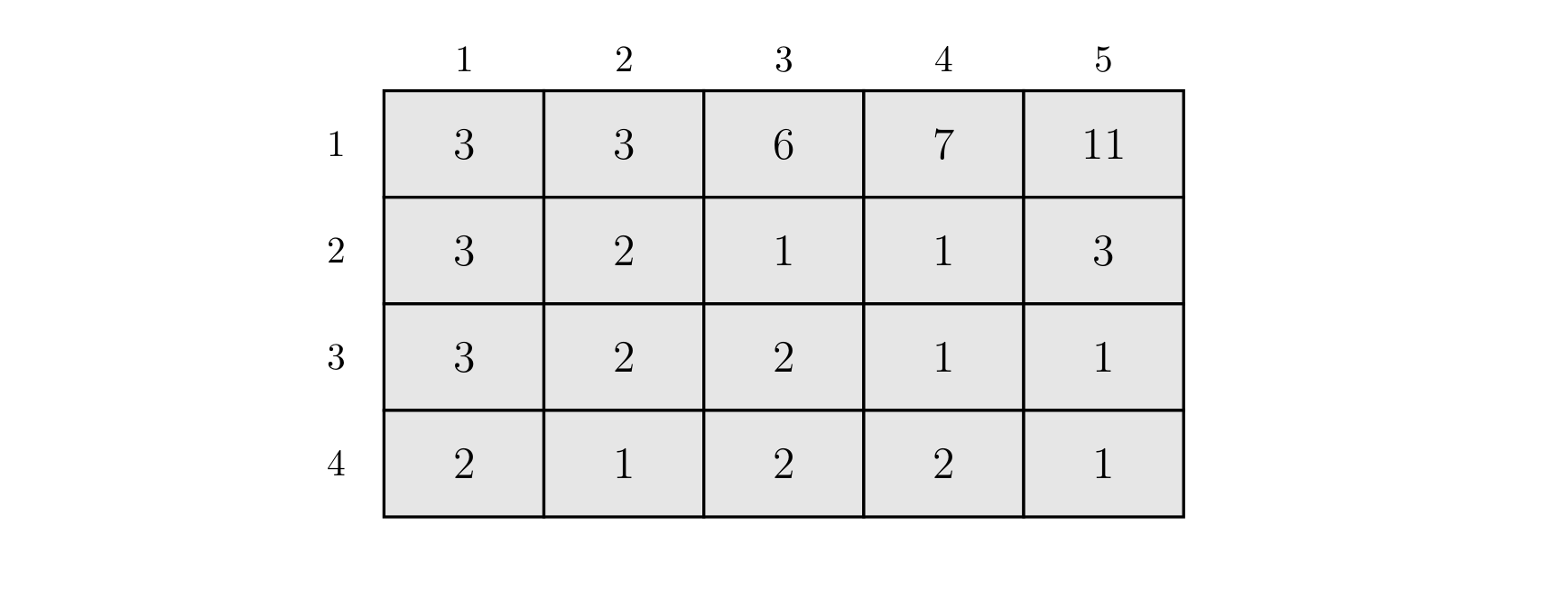For example, in the $5 \times 4$ Devil City shown above, if the explorer is currently at $(3, 3)$, then by making successive spatial jumps he can reach one of the following rooms: $(1, 1)$, $(3, 1)$, $(1, 3)$, $(5, 1)$, or $(5, 3)$. Moreover, if he wants to reach $(3, 2)$ from $(5, 4)$ in two jumps, he cannot first jump to $(4, 3)$ (because then the direction of his second jump would be the same as the first, which is not allowed). Therefore, he must first jump to $(2, 1)$. Please write a program that, for a given map, computes the minimum number of jumps the explorer needs to escape the Devil City.

The first line contains two integers $N, M$ $(1 \le N, M \le 100)$. Then follow $N$ lines, each containing $M$ natural numbers, representing the magic numbers in the corresponding rooms.

Output the minimum number of jumps. If the explorer cannot escape the Devil City, output `NEVER`.

Translated by ChatGPT 5