P13031 [GCJ 2021 #1B] Digit Blocks
题目描述
你将建造 $N$ 座塔,每座塔由 $B$ 块立方体积木组成,每次放置一块积木。塔的建造是从下往上进行的:第 $i$ 块被放置到某座塔中的积木最终会成为该塔从下往上数的第 $i$ 块。你需要在看到后续积木之前决定每块积木的放置位置,且一旦放置就不能移动。
每块积木上印有一个十进制数字,塔的建造会确保所有数字面朝前。积木的字体设计使得无法通过旋转获得不同的数字(例如,印有 6 的积木不能通过旋转变成 9,反之亦然)。
例如,假设 $N = 3$ 且 $B = 3$,当前塔的状态如图 1 所示。如果下一块积木的数字是 6,你有两种选择:要么将其放在只有两块积木的塔上(如图 2),要么开始建造第三座塔(如图 3)。注意不能将其放在第一座塔上,因为第一座塔已经有 $B$ 块积木。
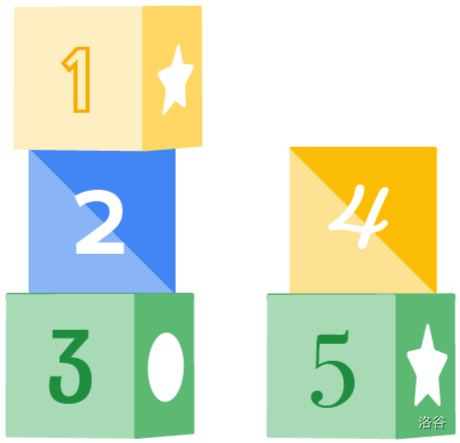
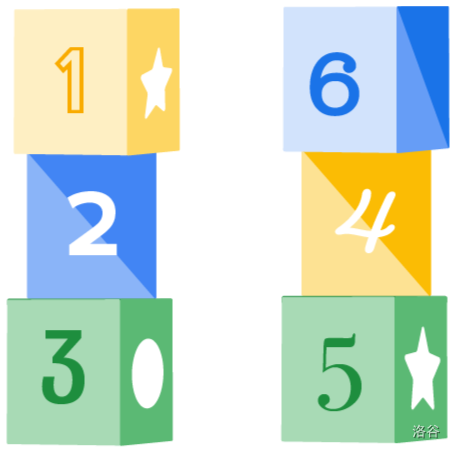

建造完成后,我们从每座塔的顶端到底端读取数字(即最后放置的积木数字是最高位),得到一个 $B$ 位整数。注意这些整数可能有任意前导零。然后,将这 $N$ 个整数相加,得到建造操作的分数。
例如,在图 4 中,从左到右的塔分别读作 $123$、$345$ 和 $96$,得分为 $123 + 345 + 96 = 564$。

每块积木的数字是独立且均匀随机生成的。为了使你的答案被判为正确,所有 $\mathbf{T}$ 个测试用例的总分必须至少达到 $\mathbf{P}$。
### 交互协议
这是一个交互问题。
最初评测机会发送一行包含四个整数 $\mathbf{T}$、$\mathbf{N}$、$\mathbf{B}$ 和 $\mathbf{P}$:测试用例数量、塔的数量、每座塔的积木数,以及通过测试集所需的最低总分。
然后,你需要处理 $\mathbf{T}$ 个测试用例。每个测试用例包含 $\mathbf{N} \times \mathbf{B}$ 次交互。每次交互对应放置一块积木。在每次交互中:
1. 评测机输出一行,包含一个整数 $\mathbf{D}$,表示当前积木的数字。
2. 你需要输出一行,包含一个整数 $\mathbf{i}$($1 \leq \mathbf{i} \leq \mathbf{N}$),表示要将积木放置到第几座塔。
在最后一个测试用例的最后一次交互后,评测机会额外输出一行:
- 如果总分 $\geq \mathbf{P}$,输出 $1$;
- 否则输出 $-1$。
如果评测机收到的交互内容格式错误、塔编号无效,或尝试将积木放到已满的塔上,它会输出 $-1$ 并终止交互。如果程序在收到 $-1$ 后仍继续等待输入,会导致超时错误(TLE)。注意:程序需要及时退出以避免 TLE,否则会被判为错误答案。
可以假设每个积木的数字是独立且均匀随机生成的,因此即使完全相同的代码提交两次,评测机也可能生成不同的随机数字。
输入格式
参见交互协议。
输出格式
参见交互协议。
说明/提示
**样例解释**
样例中的状态对应图 4(总分 = 564)。
你可以使用本地测试工具调试代码。测试工具会模拟评测机的行为,但**并非真实评测系统**,可能在某些细节上存在差异。
**数据范围**
- $\mathbf{T} = 50$
- $\mathbf{N} = 20$
- $\mathbf{B} = 15$
- $\mathbf{D}$ 是 $0$ 到 $9$ 的十进制数字
**测试集 1(16 分,可见评测结果)**
$\mathbf{P} = 860939810732536850$(约 $8.6 \times 10^{17}$)。
该边界约为理论最高期望分数($S \approx 1.9 \times 10^{16}$)的 $90\% \times \mathbf{T}$。精确的 $S$ 值可在测试工具代码的第 13-14 行找到。
**测试集 2(21 分,可见评测结果)**
$\mathbf{P} = 937467793908762347$(约 $9.37 \times 10^{17}$)。
该边界约为理论最高期望分数的 $98\% \times \mathbf{T}$。
翻译由 DeepSeek V3 完成