P13036 [GCJ 2021 #2] Matrygons

[套娃](https://en.wikipedia.org/wiki/Matryoshka_doll)是一种起源于一个多世纪前俄罗斯的玩偶。它们的显著特征是由一组大小各异的玩偶组成，较小的玩偶可以完美地嵌套在较大的玩偶内部。 在本问题中，我们研究**套娃多边形**，这是一组遵循类似嵌套规则的正则凸多边形。一个套娃多边形由一组面积为正的正则凸多边形 $p_1, p_2, \ldots, p_k$ 组成，且满足对于所有 $i$，$p_{i+1}$ 的顶点是 $p_i$ 顶点的**真子集**（即 $p_{i+1}$ 的边数严格少于 $p_i$）。 例如，下图展示了两个套娃多边形。第一个包含 3 个正则凸多边形：一个正二十四边形（24 条边）、一个正六边形（6 条边）和一个等边三角形（3 条边）。第二个包含 2 个正则凸多边形：一个正二十二边形（22 条边）和一个正十一边形（11 条边）。这两个套娃多边形的总边数均为 33。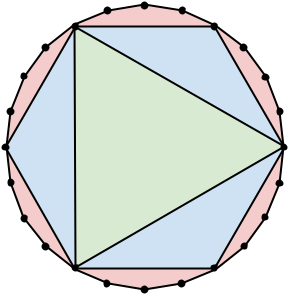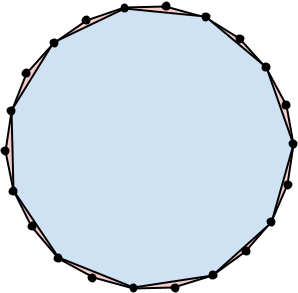   给定总边数 $\mathbf{N}$，计算在总边数恰好为 $\mathbf{N}$ 的套娃多边形中，最多可以包含多少个多边形。

输入第一行包含测试用例数量 $\mathbf{T}$。随后 $\mathbf{T}$ 行，每行一个整数 $\mathbf{N}$，表示目标总边数。

对于每个测试用例，输出一行 `Case #x: y`，其中 $x$ 为测试用例编号（从 1 开始），$y$ 为满足条件的套娃多边形中最多包含的多边形数量。

**样例解释** 问题描述中的第一个套娃多边形是样例 #1 的最优解。 在样例 #2 中，我们可以将一个正五边形（5 条边）嵌套在正十边形（10 条边）内，得到包含 2 个多边形的套娃多边形。 在样例 #3 中，无法创建包含多个正则多边形的套娃多边形，因此唯一选择是使用单个正四十一边形（41 条边）。 **限制条件** - $1 \leq \mathbf{T} \leq 100$。 **测试集 1（7 分，可见判定）** - 时间限制：20 秒。 - $3 \leq \mathbf{N} \leq 1000$。 **测试集 2（13 分，可见判定）** - 时间限制：40 秒。 - $3 \leq \mathbf{N} \leq 10^6$。 翻译由 DeepSeek V3 完成