P13036 [GCJ 2021 #2] Matrygons

A [matryoshka](https://en.wikipedia.org/wiki/Matryoshka_doll) is a type of doll that originated in Russia over a century ago. Their defining characteristic is that they consist of a set of dolls, all of a different size, with smaller dolls fitting nicely inside larger dolls. In this problem, we work with matrygons, which are sets of regular convex polygons that follow a similar nesting pattern. A matrygon consists of a set of regular convex polygons with positive area $p_1, p_2, \ldots, p_k$ such that, for all $i$, the vertices of $p_{i+1}$ overlap with a proper subset of the vertices of $p_i$ ($p_{i+1}$ has strictly less vertices than $p_i$). For example, the following pictures illustrate two matrygons. The first one contains 3 regular convex polygons: a regular icositetragon (24 sides), a regular hexagon (6 sides), and an equilateral triangle (3 sides). The second one contains 2 regular convex polygons: a regular icosidigon (22 sides) and a regular hendecagon (11 sides). Each of these matrygons has 33 total sides among all polygons in it.   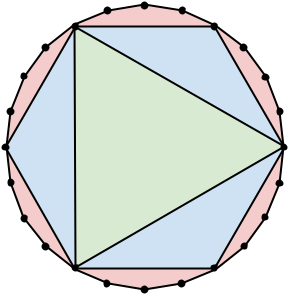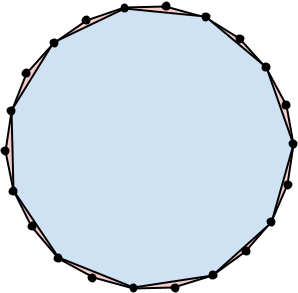Given a fixed total number of sides $\mathbf{N}$, calculate the largest number of polygons that can be part of a matrygon such that the total number of sides among all polygons in it is exactly $\mathbf{N}$.

The first line of the input gives the number of test cases, $\mathbf{T}$. $\mathbf{T}$ lines follow. Each line represents a test case and contains a single integer $\mathbf{N}$, the target total number of sides.

For each test case, output one line containing `Case #x: y`, where $x$ is the test case number (starting from 1) and $y$ is the maximum number of polygons in a matrygon such that the total number of sides among all polygons in it is exactly $\mathbf{N}$.

**Sample Explanation** The first matrygon pictured in the problem statement is an optimal solution for Sample Case #1. In Sample Case #2, we can get to two polygons by fitting a regular pentagon (5 sides) inside a regular decagon (10 sides). In Sample Case #3, there is no way to create a matrygon with multiple regular polygons, so our only option is to use a single regular tetracontahenagon (41 sides). **Limits** - $1 \leq \mathbf{T} \leq 100$. **Test Set 1 (7 Pts, Visible Verdict)** - Time limit: 20 seconds. - $3 \leq \mathbf{N} \leq 1000$. **Test Set 2 (13 Pts, Visible Verdict)** - Time limit: 40 seconds. - $3 \leq \mathbf{N} \leq 10^6$.