P13040 [GCJ 2021 #3] Square Free

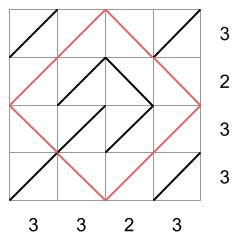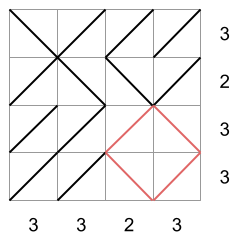
我们有一个由正方形单元格组成的矩阵，包含 $\mathbf{R}$ 行和 $\mathbf{C}$ 列。我们需要在每个单元格中绘制一条对角线。每个单元格必须且只能绘制两种对角线之一：**正斜杠对角线（/）**（连接单元格的左下角和右上角）或 **反斜杠对角线（\）**（连接单元格的左上角和右下角）。 对于每一行和每一列，我们需要绘制特定数量的正斜杠对角线。此外，在所有对角线绘制完成后，矩阵必须满足**无方格**条件。即，不能存在由所绘制的对角线构成的正方形。 例如，假设我们有一个 4 行 4 列的矩阵。每行旁边的数字表示该行必须绘制的正斜杠对角线的确切数量，每列下方的数字表示该列必须绘制的正斜杠对角线的确切数量。  存在多种方式填充该矩阵以满足每行和每列的要求。以下是三种可能的填充方式：    前两个矩阵**不满足无方格条件**，而第三个矩阵满足。在第一个矩阵中，存在一个边长为 2 的对角线组成的正方形，其顶点位于矩阵各边的中点；在第二个矩阵中，右下角存在一个边长为 1 的对角线组成的正方形；第三个矩阵则不存在任何此类正方形。因此，第三个矩阵是符合所有规则的合法填充方案。 给定矩阵的大小以及每行和每列必须绘制的正斜杠对角线的数量，请构造一个满足行和列约束的无方格矩阵，或者判断这样的矩阵不存在。

输入的第一行包含测试用例的数量 $\mathbf{T}$。接下来是 $\mathbf{T}$ 组测试用例。每组测试用例包含三行： 1. 第一行包含 $\mathbf{R}$ 和 $\mathbf{C}$，分别表示矩阵的行数和列数。 2. 第二行包含 $\mathbf{R}$ 个整数 $\mathbf{S}_1, \mathbf{S}_2, \ldots, \mathbf{S}_\mathbf{R}$，其中 $\mathbf{S}_i$ 表示第 $i$ 行（从上到下）必须绘制的正斜杠对角线的数量。 3. 第三行包含 $\mathbf{C}$ 个整数 $\mathbf{D}_1, \mathbf{D}_2, \ldots, \mathbf{D}_\mathbf{C}$，其中 $\mathbf{D}_i$ 表示第 $i$ 列（从左到右）必须绘制的正斜杠对角线的数量。

对于每组测试用例，输出一行 `Case #x: y`，其中 $x$ 是测试用例编号（从 1 开始），$y$ 为 `IMPOSSIBLE`（如果不存在满足所有规则的矩阵）或 `POSSIBLE`（如果存在）。如果输出 `POSSIBLE`，则还需额外输出 $\mathbf{R}$ 行，每行包含 $\mathbf{C}$ 个字符。其中第 $i$ 行的第 $j$ 个字符为 `/`（表示该单元格绘制正斜杠对角线）或 `\`（表示绘制反斜杠对角线）。你的方案必须满足所有规则。

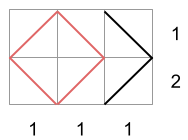
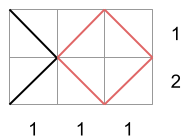
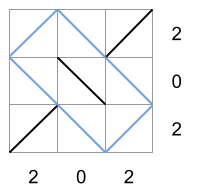
**样例解释** 样例 #1 是题目描述中提到的示例。 在样例 #2 中，根据行的总和，需要绘制 2 条正斜杠对角线，但根据列的总和，需要绘制 3 条。因此无法满足所有规则。 样例 #3 中唯一满足行和列约束的矩阵如下：    由于前两个矩阵包含正方形，第三个矩阵是唯一合法的输出。 在样例 #4 中，只有一种填充方式满足行和列约束（如下图所示）。注意，它产生了一个矩形（图中蓝色部分），但由于该矩形不是正方形，因此矩阵满足无方格条件。  **数据范围** - $1 \leq \mathbf{T} \leq 100$。 - 对于所有 $i$，$0 \leq \mathbf{S}_i \leq \mathbf{C}$。 - 对于所有 $i$，$0 \leq \mathbf{D}_i \leq \mathbf{R}$。 **测试集 1（7 分，可见判定）** - $2 \leq \mathbf{R} \leq 6$。 - $2 \leq \mathbf{C} \leq 6$。 **测试集 2（13 分，隐藏判定）** - $2 \leq \mathbf{R} \leq 20$。 - $2 \leq \mathbf{C} \leq 20$。 翻译由 DeepSeek V3 完成