P13044 [GCJ 2021 Finals] Slide Circuits

**Gooli** 是一家大型公司，在一个丘陵地区拥有 $\mathbf{B}$ 栋建筑。五年前，**Gooli** 建造了允许员工从一栋建筑滑向另一栋建筑的滑道（单向），由此开启了在建筑间建造滑道的传统。目前共有 $\mathbf{S}$ 条滑道。 **Melek** 是 **Gooli** 的交通主管，也是一位热衷解决问题的爱好者。她接到任务要保持滑道的使用乐趣。她想出的办法是禁用部分滑道，使得仅保留电路。一个电路是指由两栋或更多建筑 $b_{1}, b_{2}, \ldots, b_{k}$ 组成的集合，其中对于每个 $i$，从建筑 $b_{i}$ 到建筑 $b_{i+1}$ 恰好有一条启用的滑道，且从建筑 $b_{k}$ 到建筑 $b_{1}$ 恰好有一条启用的滑道。这些建筑的其他任何滑道都不应启用，以防止误导。此时滑道的状态被称为 **有趣状态**，当且仅当每栋建筑恰好属于一个电路。 **Gooli** 园区内的滑道用 1 到 $\mathbf{S}$ 的整数编号。**Melek** 创建了一个滑道控制台，支持两种操作：**启用** 和 **禁用**。两种操作都接收三个参数 $\ell$、$r$ 和 $m$，并对所有满足 $\ell \leq x \leq r$ 且 $x$ 是 $m$ 的倍数的滑道 $x$ 执行操作。启用操作仅在操作执行前所有受影响的滑道处于禁用状态时才有效。类似地，禁用操作仅在操作执行前所有受影响的滑道处于启用状态时才有效。 下图展示了可能的操作序列和状态变化。布局包含 3 栋建筑和 3 条滑道。禁用状态的滑道显示为浅灰色，启用状态的滑道显示为深灰色。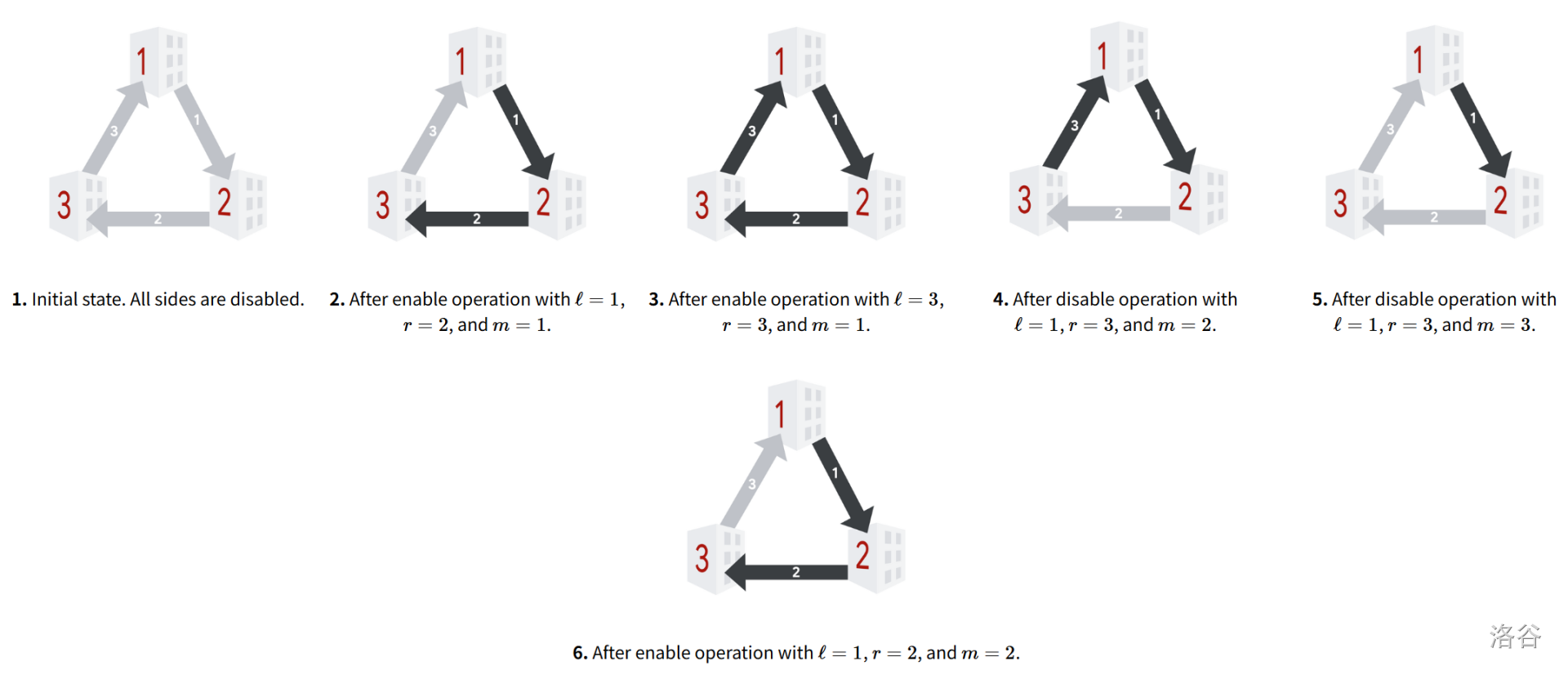  1. 初始状态。所有滑道禁用。 2. 执行启用操作 $\ell=1$，$r=2$，$m=1$ 后。 3. 执行启用操作 $\ell=3$，$r=3$，$m=1$ 后。 4. 执行禁用操作 $\ell=1$，$r=3$，$m=2$ 后。 5. 执行禁用操作 $\ell=1$，$r=3$，$m=3$ 后。 6. 执行启用操作 $\ell=1$，$r=2$，$m=2$ 后。 不幸的是，**Melek** 的猫 **Sult** 发现了控制台，并开始执行一系列有效的启用和禁用操作。在 **Sult** 执行每次操作后，**Melek** 想知道是否可以通过 **恰好启用一条当前禁用的滑道** 使滑道达到有趣状态。注意 **Melek** 实际上并不会启用这条滑道。 在上图中可以看到，在第一次、第三次和最后一次操作后，**Melek** 可以启用唯一禁用的滑道，使状态变为有趣状态。第二次操作后存在两个问题：一是当前没有禁用的滑道，因此 **Melek** 无法启用任何滑道；此外，状态已经是有趣状态，即使有其他禁用的滑道，启用任何滑道都会导致状态不再有趣。第四次操作后，有两条禁用的滑道，但启用任意一条都无法得到有趣状态。 所有滑道最初都是禁用的，然后 **Sult** 依次执行操作。在 **Sult** 的每次操作后，确定 **Melek** 可以启用哪条禁用的滑道（如果有的话）使滑道达到有趣状态。

输入的第一行包含测试用例的数量 $\mathbf{T}$。随后是 $\mathbf{T}$ 个测试用例。每个测试用例的第一行包含三个整数 $\mathbf{B}$、$\mathbf{S}$ 和 $\mathbf{N}$，分别表示建筑数量、滑道数量和处理的操作数量。接下来 $\mathbf{S}$ 行，每行包含两个整数 $\mathbf{X}_{i}$ 和 $\mathbf{Y}_{i}$，表示编号为 $i$ 的滑道从建筑 $\mathbf{X}_{i}$ 通向建筑 $\mathbf{Y}_{i}$。最后 $\mathbf{N}$ 行描述操作。第 $j$ 行包含一个字符 $\mathbf{A}_{j}$ 和三个整数 $\mathbf{L}_{j}$、$\mathbf{R}_{j}$ 和 $\mathbf{M}_{j}$，描述第 $j$ 个操作。$\mathbf{A}_{j}$ 表示操作类型，大写字母 $\mathbf{E}$ 表示启用，大写字母 $\mathbf{D}$ 表示禁用。操作会对所有编号是 $\mathbf{M}_{j}$ 的倍数且介于 $\mathbf{L}_{j}$ 和 $\mathbf{R}_{j}$ 之间的滑道执行。

对于每个测试用例，输出一行 `Case #x:` $y_{1} y_{2} ... y_{N}$，其中 $x$ 是测试用例编号（从 1 开始），$y_{j}$ 是一个大写字母 $\mathbf{X}$（如果在前 $j$ 次操作后无法通过启用恰好一条禁用滑道使状态变为有趣状态），否则 $y_{j}$ 是一个整数，表示启用编号为 $y_{j}$ 的滑道可以使前 $j$ 次操作后的状态变为有趣状态。

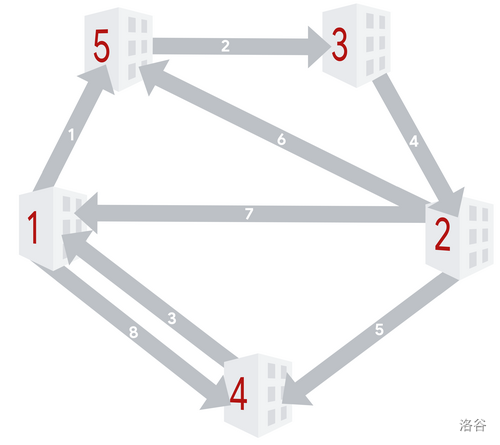
**样例解释** 样例 #1 对应题目描述中的图示案例。 下图展示了样例 #2 的建筑和滑道布局：  每次操作后启用的滑道集合依次为： 1. $\{2,4,6,8\}$ 2. $\{2\}$ 3. $\{2,3,4,5\}$ 4. $\{2,3,4,5\}$ 5. $\{1,2,3,4,5\}$ 6. $\{1,2,3,4,5,6,8\}$ 7. $\{1,2,4,5,8\}$ 8. $\{1,2,4,5\}$ 9. $\{1,2\}$ 10. $\{1,2,3,4\}$ **数据范围** - 对所有 $i$，$1 \leq \mathbf{X}_{i} \leq \mathbf{B}$ - 对所有 $i$，$1 \leq \mathbf{Y}_{i} \leq \mathbf{B}$ - 对所有 $i$，$\mathbf{X}_{i} \neq \mathbf{Y}_{i}$ - 对所有 $i \neq j$，$\left(\mathbf{X}_{i}, \mathbf{Y}_{i}\right) \neq\left(\mathbf{X}_{j}, \mathbf{Y}_{j}\right)$ - 对所有 $j$，$\mathbf{A}_{j}$ 为大写字母 $\mathbf{E}$ 或 $\mathbf{D}$ - 对所有 $j$，$1 \leq \mathbf{L}_{j} \leq \mathbf{R}_{j} \leq \mathbf{S}$ - 对所有 $j$，$1 \leq \mathbf{M}_{j} \leq \mathbf{S}$ - 每个操作都有效 **测试集 1（10 分，可见判定）** - 时间限制：10 秒 - $1 \leq \mathbf{T} \leq 100$ - $2 \leq \mathbf{B} \leq 100$ - $2 \leq \mathbf{S} \leq 1000$ - $1 \leq \mathbf{N} \leq 1000$ **测试集 2（20 分，隐藏判定）** - 时间限制：120 秒 - $1 \leq \mathbf{T} \leq 30$ - $2 \leq \mathbf{B} \leq 3 \times 10^{4}$ - $2 \leq \mathbf{S} \leq 3 \times 10^{5}$ - $1 \leq \mathbf{N} \leq 3 \times 10^{5}$ 翻译由 DeepSeek V3 完成