P13047 [GCJ 2021 Finals] Infinitree

本题需要计算一棵严格二叉树上两个节点之间的距离。哦，这太简单了？！好吧，现在这棵树可能是无限的。继续努力的话，我们可能要开始讨论阿列夫数了。 在这道题中，一棵树要么是一个单独的节点 $X$，要么是一个节点 $X$ 附带两棵子树：左子树和右子树。无论是哪种情况，$X$ 都是这棵树的根节点。如果树不是单个节点，那么左子树和右子树的根节点是 $X$ 仅有的两个子节点。 有一组颜色编号从 0 到 $\mathbf{N}$（包括 $\mathbf{N}$）。每个节点恰好有一种颜色。每种颜色可能有零个、一个或多个节点。颜色为 0（白色）的节点是叶节点（即没有子节点）。对于颜色为 $i$（$1 \leq i \leq \mathbf{N}$）的节点，它恰好有两个子节点：左子节点的颜色为 $\mathbf{L}_{i}$，右子节点的颜色为 $\mathbf{R}_{i}$。树的根节点颜色为 1（黑色）。注意，这棵树的节点数量可能是有限的或可数无限的。 例如，下图展示了一棵由列表 $\mathbf{L}=[3,0,0]$ 和 $\mathbf{R}=[2,0,2]$ 定义的有限树。颜色 2 为蓝色，颜色 3 为黄色。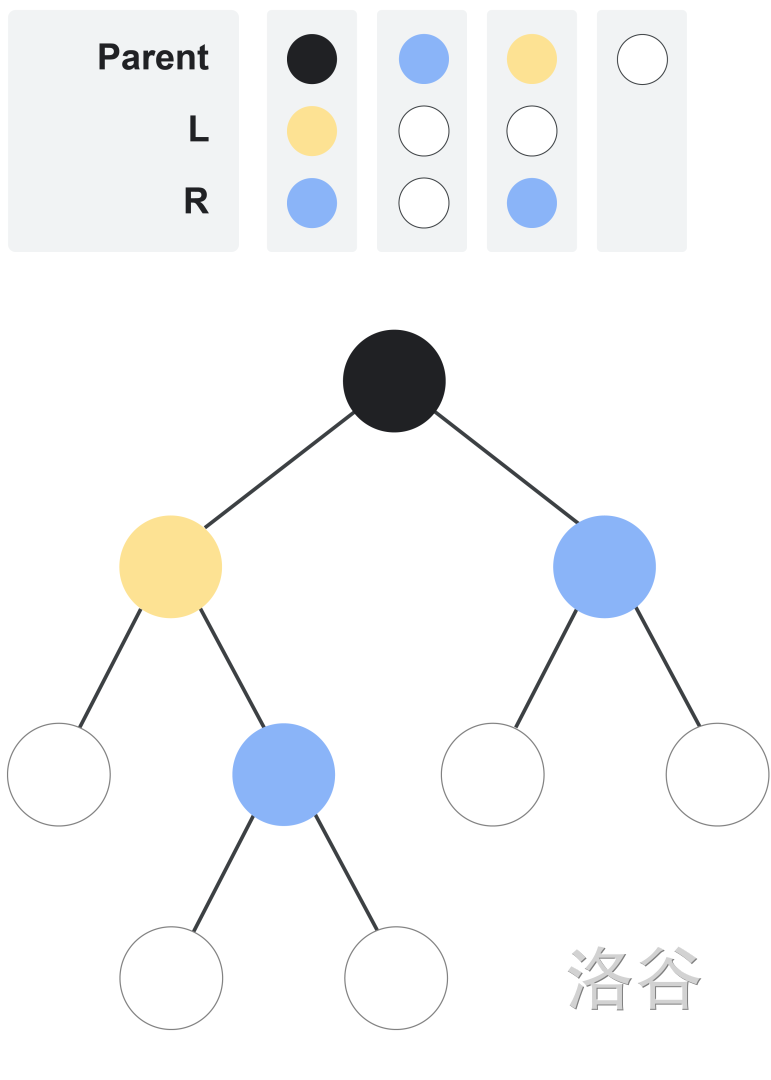  树中两个节点之间的距离是从一个节点到另一个节点所需的最少步数。每一步可以是从一个节点移动到其直接父节点或直接子节点。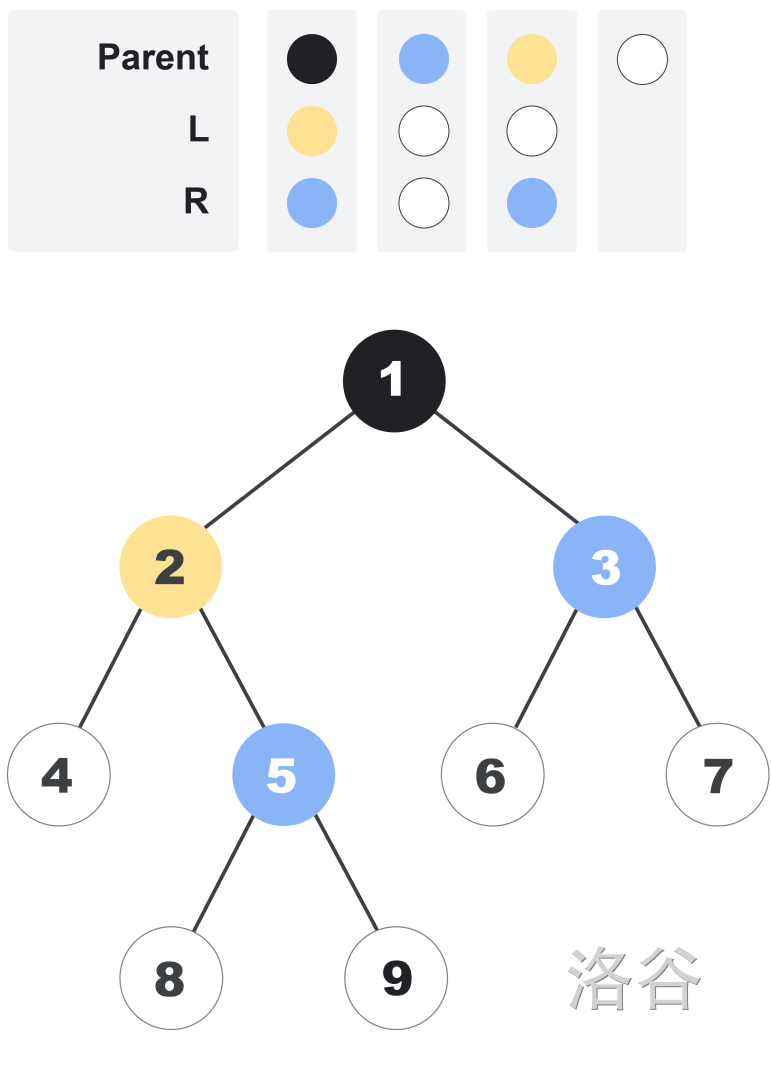 树中的节点用正整数编号。根节点的编号为 $1$。其他节点按以下规则编号：距离根节点较近的节点优先编号；若距离相同，则左侧的节点优先编号。例如，下图展示了之前那棵树中每个节点的编号。注意，每个节点的编号与其颜色无关。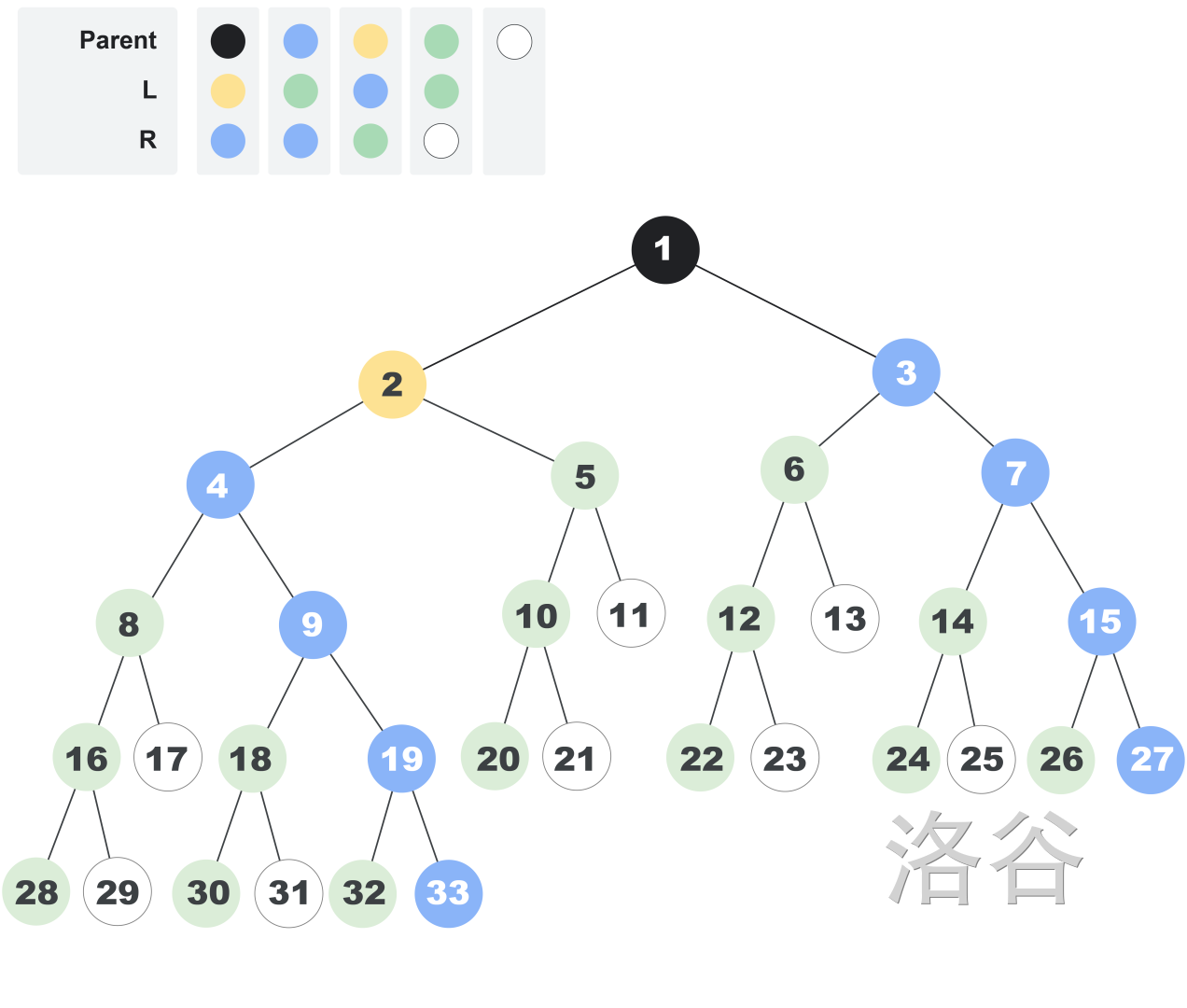  再举一个例子，下图展示了由列表 $\mathbf{L}=[3,4,2,4]$ 和 $\mathbf{R}=[2,2,4,0]$ 定义的无限树的前 $33$ 个节点。颜色 4 为绿色。  给定定义树的列表 $\mathbf{L}$ 和 $\mathbf{R}$，以及树中两个不同节点的编号，返回这两个节点之间的距离。

输入的第一行包含测试用例的数量 $\mathbf{T}$。随后 $\mathbf{T}$ 个测试用例，每个测试用例包含三行。第一行包含 $\mathbf{N}$、$\mathbf{A}$ 和 $\mathbf{B}$：分别表示定义树的列表的大小，以及需要计算距离的两个节点的编号。第二行包含 $\mathbf{N}$ 个整数 $\mathbf{L}_{1}, \mathbf{L}_{2}, \ldots, \mathbf{L}_{\mathbf{N}}$，第三行包含 $\mathbf{N}$ 个整数 $\mathbf{R}_{1}, \mathbf{R}_{2}, \ldots, \mathbf{R}_{\mathbf{N}}$，如上所述。

对于每个测试用例，输出一行 `Case #x: y`，其中 $x$ 为测试用例编号（从 1 开始），$y$ 为由 $\mathbf{L}$ 和 $\mathbf{R}$ 定义的树中编号为 $\mathbf{A}$ 和 $\mathbf{B}$ 的两个节点之间的距离。

**样例解释** 样例 #1 和 #2 中的树是题目描述中的第一棵树。样例 #3 和 #4 中的树是题目描述中的最后一棵树。样例 #5 中，注意某些颜色可能在树中不存在。 样例测试集 2 符合测试集 2 的限制条件，但不会对提交的解决方案运行。 **数据范围** - $1 \leq \mathbf{T} \leq 100$。 - $1 \leq \mathbf{N} \leq 50$。 - $0 \leq \mathbf{L}_{i} \leq \mathbf{N}$。 - $0 \leq \mathbf{R}_{i} \leq \mathbf{N}$。 - $\mathbf{A} < \mathbf{B} \leq 10^{18}$。 - 由 $\mathbf{L}$ 和 $\mathbf{R}$ 定义的树至少有 $\mathbf{B}$ 个节点。 **测试集 1（25 分，可见判定）** - $\mathbf{A} = 1$。 **测试集 2（40 分，隐藏判定）** - $1 \leq \mathbf{A} \leq 10^{18}$。 翻译由 DeepSeek V3 完成