P13054 [GCJ 2020 #1A] Pascal Walk

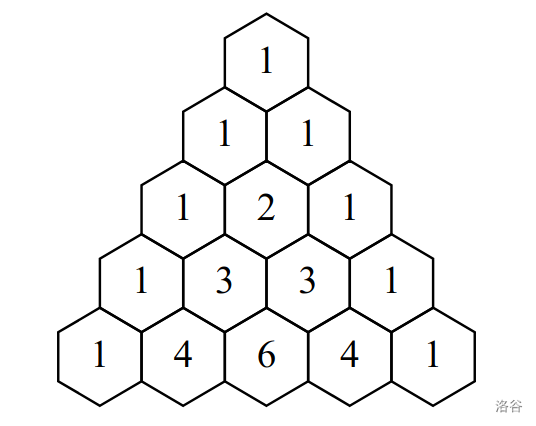
**帕斯卡三角形** 由无限多行整数构成，每行的整数数量逐行递增，排列成三角形。 定义 $(r, k)$ 为第 $r$ 行从左数第 $k$ 个位置，其中 $r$ 和 $k$ 均从 1 开始计数。帕斯卡三角形的构造遵循以下规则： - 第 $r$ 行包含 $r$ 个位置 $(r, 1), (r, 2), \ldots, (r, r)$。 - 对于所有 $r$，位置 $(r, 1)$ 和 $(r, r)$ 的数字均为 $1$。 - 对于所有满足 $2 \leqslant k \leqslant r-1$ 的 $k$，位置 $(r, k)$ 的数字等于位置 $(r-1, k-1)$ 和 $(r-1, k)$ 的数字之和。 帕斯卡三角形的前 5 行如下所示：  在本问题中，**帕斯卡游走** 是指帕斯卡三角形中一个长度为 $\mathrm{s}$ 的位置序列 $\left(\mathrm{r}_{1}, \mathrm{k}_{1}\right), \left(\mathrm{r}_{2}, \mathrm{k}_{2}\right), \ldots, \left(\mathrm{r}_{\mathrm{s}}, \mathrm{k}_{\mathrm{s}}\right)$，满足以下条件： 1. $\mathrm{r}_{1}=1$ 且 $\mathrm{k}_{1}=1$。 2. 每个后续位置必须在三角形内，并且与前一个位置相邻（六个可能方向之一）。即对于所有 $\mathrm{i} \geqslant 1$，$\left(\mathrm{r}_{\mathrm{i}+1}, \mathrm{k}_{\mathrm{i}+1}\right)$ 必须是以下之一且位于三角形内：$\left(\mathrm{r}_{\mathrm{i}}-1, \mathrm{k}_{\mathrm{i}}-1\right)$、$\left(\mathrm{r}_{\mathrm{i}}-1, \mathrm{k}_{\mathrm{i}}\right)$、$\left(\mathrm{r}_{\mathrm{i}}, \mathrm{k}_{\mathrm{i}}-1\right)$、$\left(\mathrm{r}_{\mathrm{i}}, \mathrm{k}_{\mathrm{i}}+1\right)$、$\left(\mathrm{r}_{\mathrm{i}}+1, \mathrm{k}_{\mathrm{i}}\right)$、$\left(\mathrm{r}_{\mathrm{i}}+1, \mathrm{k}_{\mathrm{i}}+1\right)$。 3. 序列中不能重复访问同一位置。即对于任意 $\mathrm{i} \neq \mathrm{j}$，必须满足 $\mathrm{r}_{\mathrm{i}} \neq \mathrm{r}_{\mathrm{j}}$ 或 $\mathrm{k}_{\mathrm{i}} \neq \mathrm{k}_{\mathrm{j}}$，或两者均不相等。 请构造一个长度 $\mathrm{S} \leqslant 500$ 的帕斯卡游走，使得所访问位置中所有数字之和恰好等于 $\mathrm{N}$。题目保证对于所有 $\mathrm{N}$，至少存在一个这样的游走。

输入的第一行包含测试用例数量 $\mathrm{T}$。随后是 $\mathrm{T}$ 个测试用例，每个用例占一行，包含一个整数 $\mathrm{N}$。

对于每个测试用例，首先输出一行 `Case #x:`，其中 $\mathrm{x}$ 为测试用例编号（从 1 开始）。接着输出你构造的帕斯卡游走，共 $\mathrm{S} \leqslant 500$ 行，每行格式为 $\mathrm{r}_{\mathrm{i}} \ \mathrm{k}_{\mathrm{i}}$，表示游走的第 $\mathrm{i}$ 个位置 $\left(\mathrm{r}_{\mathrm{i}}, \mathrm{k}_{\mathrm{i}}\right)$。例如，第一行必须为 `1 1`，因为所有有效游走的起点均为 $(1,1)$。游走中所有位置的数字之和必须严格等于 $\mathrm{N}$。

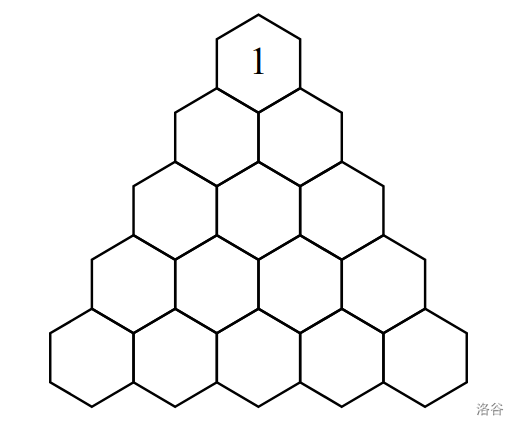
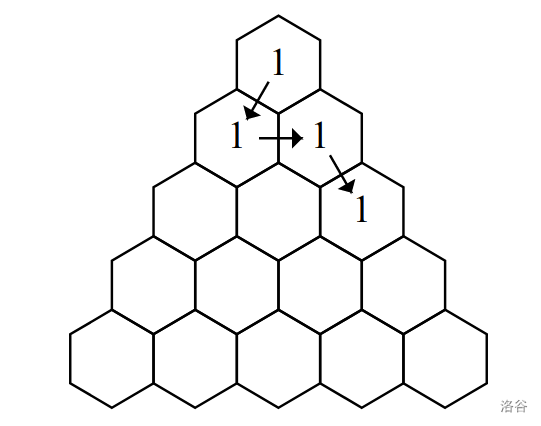
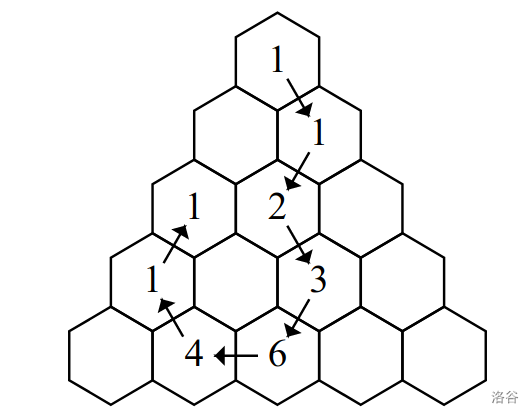
## 说明/提示 **样例解释** - 样例 #1 仅需起点位置即可满足要求。  - 样例 #2 中，虽然存在更短的路径，但路径长度只需不超过 500 即可，无需最短。  - 下图展示了样例 #3 的解决方案：  **数据范围** - $1 \leqslant \mathrm{T} \leqslant 100$。 **测试集 1（3 分，可见评测结果）** - $1 \leqslant \mathrm{N} \leqslant 501$。 **测试集 2（11 分，可见评测结果）** - $1 \leqslant \mathrm{N} \leqslant 1000$。 **测试集 3（21 分，隐藏评测结果）** - $1 \leqslant \mathrm{N} \leqslant 10^{9}$。 翻译由 DeepSeek V3 完成