P13063 [GCJ 2020 #2] Security Update

**Apricot Rules** 公司刚刚在其网络上安装了一个关键的安全更新。该网络有一台源计算机，其他所有计算机都通过一条或多条直接双向连接与源计算机相连。 这种更新会自行传播：一旦某台计算机首次接收到更新，它会立即开始向所有直接连接的计算机传输更新。每条直接连接都有一个延迟值：表示该连接传输更新所需的秒数（双向传输的延迟相同）。因此，更新不会瞬间传播到所有计算机。 **Apricot Rules** 的工程师不知道这些延迟的具体值，但他们知道这些值都是正整数。他们希望你能根据最近一次实验中观察到的更新传播情况，推断出这些延迟的可能取值。 工程师仅在源计算机上安装了更新，然后等待更新传播到整个系统，直到所有计算机都完成更新。他们记录了更新传播的一些信息。具体来说，对于除源计算机外的每台计算机 $K$，你确切知道以下两种情况之一： - 源计算机接收到更新的时间与 $K$ 首次接收到更新的时间之间的精确秒数。 - 在 $K$ 首次接收到更新之前，严格比 $K$ 更早接收到更新的其他计算机（包括源计算机）的数量。 注意，多台计算机可能在同一时间接收到更新。 你需要为每对直接连接的计算机计算一个延迟值（单位为秒）。每个延迟值必须是一个不超过 $10^6$ 的正整数。你提供的延迟值集合必须与所有已知信息一致。题目保证至少存在一种一致的延迟分配方式。

输入的第一行包含测试用例的数量 $T$。接下来是 $T$ 个测试用例。每个测试用例的第一行包含两个整数 $C$ 和 $D$，分别表示计算机的数量和直接连接的数量。计算机编号为 $1$ 到 $C$，其中计算机 $1$ 是源计算机。 第二行包含 $C-1$ 个整数 $X_2$, $X_3$, $\dots$, $X_C$。如果 $X_i$ 为正，表示计算机 $i$ 在计算机 $1$ 接收到更新后的 $X_i$ 秒接收到更新；如果 $X_i$ 为负，表示 $-X_i$ 台其他计算机（包括源计算机）在计算机 $i$ 之前严格更早接收到更新。 接下来的 $D$ 行表示网络中的 $D$ 条直接连接。第 $i$ 行包含两个整数 $U_i$ 和 $V_i$，表示计算机 $U_i$ 和 $V_i$ 直接相连。

对于每个测试用例，输出一行 `Case #x: y_1 y_2 ... y_D`，其中 $x$ 是测试用例编号（从 $1$ 开始），$y_i$ 是一个不超过 $10^6$ 的正整数，表示分配给第 $i$ 条直接连接的延迟值（单位为秒）。

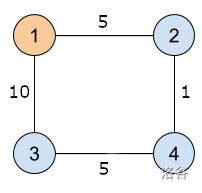
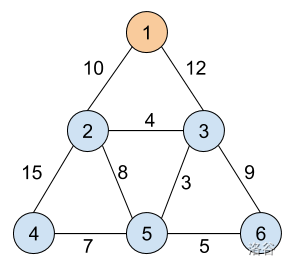
**样例解释** 在样例 #1 中，下图展示了样例输出对应的计算机网络。标有 $i$ 的圆圈表示第 $i$ 台计算机，连接两个圆圈的线表示直接连接，线上的数字表示该连接的延迟值。  在样例 #2 中，前三条连接的延迟必须相同，而第四条连接的延迟可以是任意有效值。注意，$-2$、$0$、$1000001$ 和 $3.14$ 都是无效的延迟值。 在样例 #3 中，由于连接是双向的，更新可以从计算机 $3$ 传输到计算机 $2$。任意两个有效的延迟值均可满足条件。 样例测试集 #2 不会出现在测试集 #1 中，但可能出现在测试集 #2 中。 其中一个正确的输出是 $10\ 12\ 4\ 15\ 8\ 3\ 9\ 7\ 5$，如下图所示。  **数据范围** - $1 \leq T \leq 100$。 - $2 \leq C \leq 100$。 - $C - 1 \leq D \leq 1000$。 - 对于所有 $i$，$1 \leq U_i < V_i \leq C$。 - 对于所有 $i \neq j$，$(U_i, V_i) \neq (U_j, V_j)$。 - 所有计算机（除源计算机外）都通过一条或多条直接连接与源计算机相连。 - 至少存在一种与输入一致的延迟分配方式。 **测试集 1（9 分，可见评测结果）** - 对于所有 $i$，$-C < X_i < 0$（即所有计算机的信息均为第二种类型）。 **测试集 2（11 分，隐藏评测结果）** - 对于所有 $i$，$-C < X_i \leq 1000$。 - 对于所有 $i$，$X_i \neq 0$。 翻译由 DeepSeek V3 完成