P13069 [GCJ 2020 #3] Recalculating

你为 Apricot Rules LLC 公司的**无人驾驶直送无人机导航设计部**工作。公司即将推出首款无人机"Principia"，你需要为其设计备用导航系统，以防其失去主要定位系统（如 GPS）后仍能获取方向指引。Principia 设计用于平面区域，该区域被建模为笛卡尔坐标系（单位为米），坐标系中分布着一个或多个无人机维修中心，且任意两个维修中心位置不同。 Principia 配备的系统可获取其当前位置 $L_1$ 距离（曼哈顿距离）不超过 $\mathbf{D}$ 米范围内的维修中心相对位置信息。例如："有一个维修中心在正北 4 米、正西 3.5 米处，另一个在正东 2.5 米处"。注意这些信息不标识具体维修中心，仅提供相对于 Principia 的位置。 你很快意识到，地图上可能存在某些点无法通过这些信息唯一确定当前位置，因为不同位置可能产生相同的相对信息集。这类点称为**不可区分点**，其余点称为**可区分点**。 形式化定义：当 Principia 位于 $(x, y)$ 时，获取的信息 $\text{Info}(x, y)$ 是所有满足 $|z - x| + |w - y| \leq \mathbf{D}$ 的维修中心坐标 $(z, w)$ 对应的相对位置 $(z - x, w - y)$ 的集合。若存在另一个点 $(x_2, y_2)$ 使得 $\text{Info}(x_1, y_1) = \text{Info}(x_2, y_2)$，则 $(x_1, y_1)$ 是不可区分点。 例如：设 $\mathbf{D} = 4$，维修中心位于 $(0, 0)$ 和 $(5, 0)$。点 $(0, 0)$ 不可区分，因为 $\text{Info}(0, 0) = \{(0, 0)\} = \text{Info}(5, 0)$。而 $(3.5, 0.1)$ 是可区分点，因其信息集 $\{(-3.5, -0.1), (1.5, -0.1)\}$ 唯一。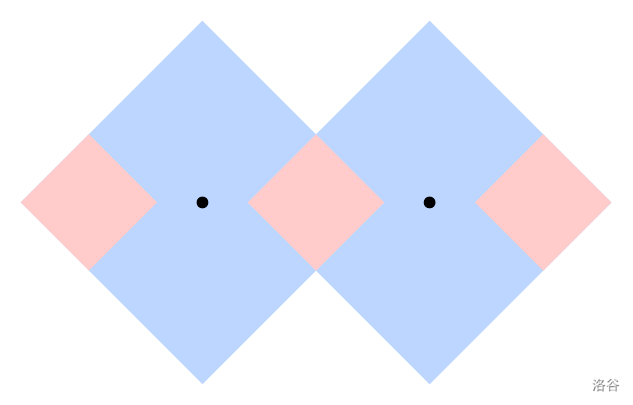下图展示了可区分点（红色）与不可区分点（蓝色）的分布：  Principia 的部署位置从所有满足 $\text{Info}(x, y)$ 非空的点中均匀随机选择。连续点集 $S$ 的被选概率与其面积（平方米）成正比。上例中每个红色区域面积为 4.5 平方米，蓝色区域为 23 平方米，因此部署到红色区域的概率为 $4.5 / (3 \times 4.5 + 2 \times 23)$，蓝色区域为 $23 / (3 \times 4.5 + 2 \times 23)$。边界区域面积为 0，被选概率严格为 0。 给定所有维修中心坐标，求 Principia 被部署到可区分点的概率。

第一行输入测试用例数 $\mathbf{T}$。每个测试用例包含： - 两个整数 $\mathbf{N}$（维修中心数量）和 $\mathbf{D}$（最大 $L_1$ 距离） - $\mathbf{N}$ 行，每行两个整数 $\mathbf{X_i}, \mathbf{Y_i}$ 表示维修中心坐标（单位：米）

对每个测试用例，输出 `Case #x: y z`，其中 $y/z$ 为最简分数形式的概率（$z$ 取最小可能值）。

**样例解释** 样例测试集 1 符合测试集 1 的限制条件。其他不符合该限制的样例可能出现在任意其他测试集中。 样例 #1 已在题目描述中详细说明并配有图示。 中间红色区域的所有点都是可区分点，因为它们是唯一能同时获取两个维修中心信息的点，且该区域内每个点获取的信息集都是唯一的。 左右两侧红色区域的点各自只能获取一个维修中心的信息，但这些信息始终是唯一的，因此也都是可区分点。例如，若 Principia 知道自己在某个维修中心东侧 $3$ 米处，可以确定这不是 $(0, 0)$ 维修中心的东侧 $3$ 米（否则会同时获取两个维修中心的信息），因此必定是 $(5, 0)$ 维修中心的东侧 $3$ 米。 蓝色区域的所有点都是不可区分点。任选其中一个区域内的点，Principia 获取的信息仅包含范围内单个维修中心的数据，但在另一个蓝色区域存在对应点会生成完全相同的信息集。 如前所述，Principia 部署到单个红色区域的概率为 $4.5/59.5$，因此部署到任意红色区域的总概率为 $3\times 4.5/59.5 = 27/119$。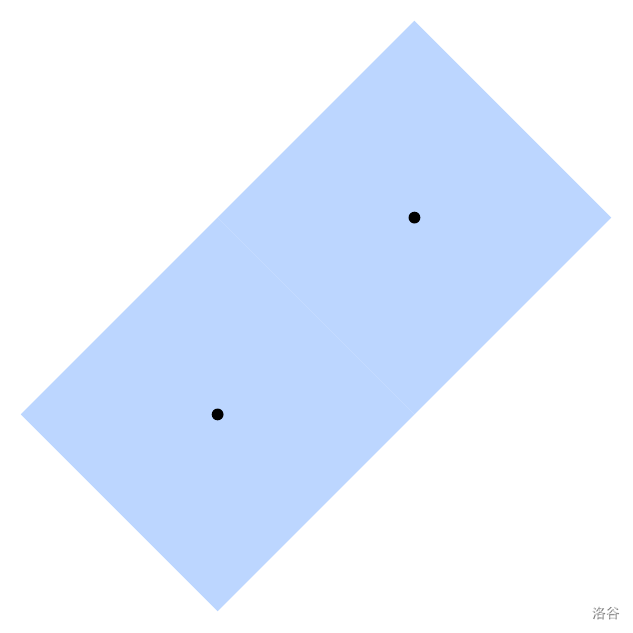 下图展示样例 #2。由于无法获取超过一个维修中心的信息，所有靠近维修中心的点都是不可区分的——从另一个维修中心附近的对应点会获取完全相同的信息。注意分母 $z$ 必须取最小值，因此 $0\ 1$ 是唯一可接受的答案。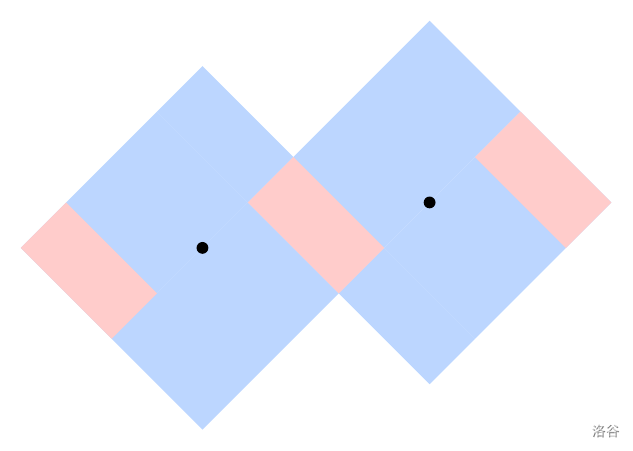  下图展示样例 #3。注意两个蓝色方形交界处的边界点属于可区分点，但由于其面积为 $0$，被部署到该处的概率为 $0$。其余所有可部署点都是不可区分的。  下图展示样例 #4。  下图展示附加测试用例。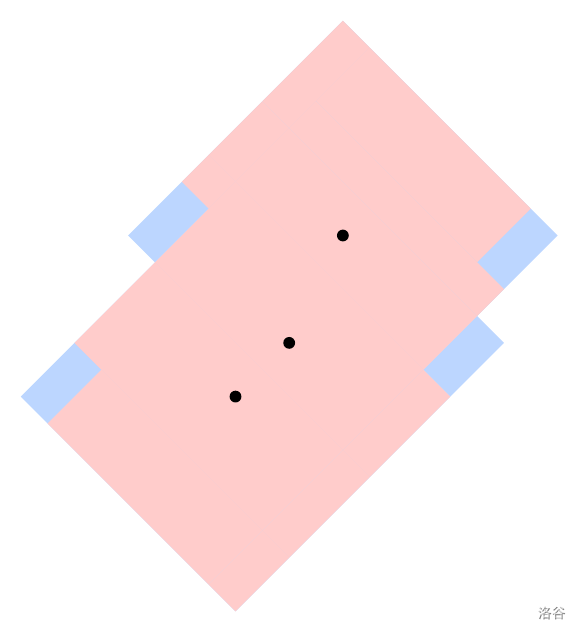  **数据范围** - $1 \leq \mathbf{T} \leq 100$ - $1 \leq \mathbf{D} \leq 10^7$ - 对所有 $i$，$-10^9 \leq \mathbf{X_i} \leq 10^9$ - 对所有 $i$，$-10^9 \leq \mathbf{Y_i} \leq 10^9$ - 对所有 $i \neq j$，$(\mathbf{X_i}, \mathbf{Y_i}) \neq (\mathbf{X_j}, \mathbf{Y_j})$（任意两个维修中心位置不同） **测试集 1（6 分，可见判定）** - 时间限制：20 秒 - $\mathbf{N} = 2$ **测试集 2（11 分，可见判定）** - 时间限制：60 秒 - $2 \leq \mathbf{N} \leq 10$ **测试集 3（15 分，可见判定）** - 时间限制：120 秒 - 其中 6 个用例 $\mathbf{N} = 1687$ - 其余 $\mathbf{T}-6$ 个用例 $2 \leq \mathbf{N} \leq 100$ 翻译由 DeepSeek V3 完成