P13082 [NOISG 2017] Hotspot / 热门地点
题目背景
译自 [NOISG 2017 C.Hotspot](https://github.com/noisg/sg_noi_archive/tree/master/2017/hotspot)。
题目描述
一个国家有 $n$ 个城镇,这些城镇由 $m$ 条长度相同的道路连接。
这个国家有 $k$ 个公民。有趣的是,第 $i$ 位公民的家和办公室位于两个不同的城镇 $A_i$ 和 $B_i$。因此,第 $i$ 个公民每天都会在 $A_i$ 和 $B_i$ 两个固定的城镇间往返。
为了节省时间,第 $i$ 个公民将选择长度最短的路径。如果 $A_i$ 和 $B_i$ 间有多条最短路径,他 / 她将随机选择一条最短路径。第 $i$ 个公民通过城镇 $w$ 的期望为:
$$E_i(w)=\dfrac{S_w(A_i,B_i)}{S(A_i,B_i)}$$
其中 $S(u,v)$ 表示 $u$ 和 $v$ 间的最短路数量,$S_w(u,v)$ 表示 $u$ 和 $v$ 间经过 $w$ 的的最短路数量。
小 D 是这个国家的总统。他想了解公民的需求,于是想在国家的某一个城镇上设立一个会议办公室,因为这样他就可以会见尽可能多的公民。确切地说,他想将会议办公室设立在使 $\sum\limits_{i=0}^{k-1}E_i(w)$ 最大的城镇 $w$。
你的任务是帮助小 D 找到符合要求的 $w$。当有多个符合要求的城镇 $w$ 时,你可以输出其中的任何一个。
注意本题需要使用**双精度浮点数**。
输入格式
第一行两个正整数 $n,m$,分别表示城镇和道路的数量。
接下来 $m$ 行,每行两个整数 $u,v$,表示城镇 $u$ 和城镇 $v$ 间有一条道路相连。
接下来一行包含一个正整数 $k$,表示公民的个数。
接下来 $k$ 行,第 $i$ 行两个整数 $A_i,B_i$,表示第 $i$ 个公民的家和办公室的位置。
输出格式
一行一个整数表示使 $\sum\limits_{i=0}^{k-1}E_i(w)$ 最大的城镇 $w$。如果有多个符合要求的解,输出其中的任何一个即可。
说明/提示
### 样例解释
对于样例 1 和 3,显然选择城镇 $3$ 也是正确的。
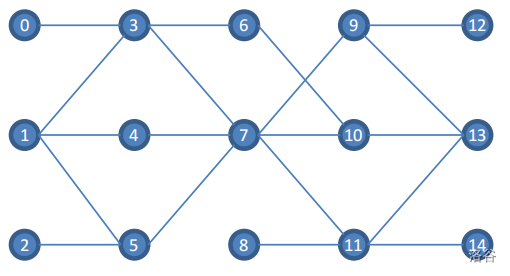
对于样例 4(如下图),在城镇 $4$ 和城镇 $10$ 之间只有一条长度为 $2$ 的最短路径,即 $4\to7\to10$。此外,城镇 $3$ 和城镇 $8$ 之间只有一条长度为 $3$ 的最短路径,即 $3\to7\to11\to8$。
如果小 D 在城镇 $7$ 建造会议办公室,那么 $\sum\limits_{i=0}^{k-1}E_i(w)=2$ 最大。
### 数据范围
请注意本题时限为 $2.5$ 秒。
**本题采用 $\text{Subtask}$ 捆绑测试。**
|$\text{Subtask}$|分值|性质|
|:-:|:-:|:-:|
|$1$|$4$|图是一条链,且 $n\le1000$,$m=n-1$,$k=1$|
|$2$|$5$|图是一棵树,且 $n\le1000$,$m=n-1$,$k=1$|
|$3$|$11$|图是一条链,且 $n\le1000$,$m=n-1$,$k\le200$|
|$4$|$18$|图是一棵树,且 $n\le1000$,$m=n-1$,$k\le200$|
|$5$|$26$|$n\le1000$,$m\le8000$,$k\le20$|
|$6$|$36$|$1\le n\le5000$,$1\le m\le 4\times 10^4$,$1\le k \le2000$|
对于所有数据,保证 $1\le n\le5000$,$1\le m\le 4\times 10^4$,$1\le k \le2000$,$1\le u,v,A_i,B_i\le n$,任何两个城镇之间的最短路不会超过 $2^{15}$ 条。